Question

Due to friction, the system as shown in the diagram remains motionless. Calculate the static coefficient of friction?

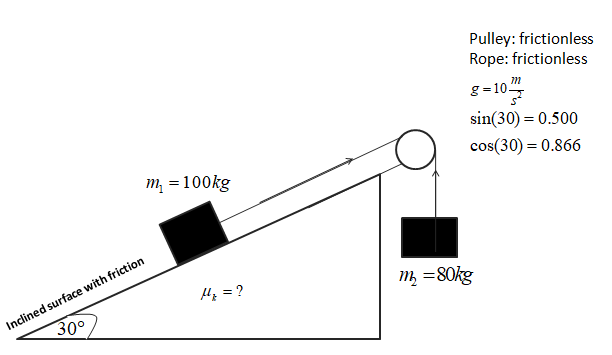
Answer 1

Hint:First, the weights of the given masses have to be divided into two components: horizontal and vertical. Thereafter, the forces acting on the masses have to be concluded. The formula of the frictional force has to be known in terms of the static coefficient of friction. The value of the static coefficient of friction can be found in the equation of forces.

Formula used:
The static frictional force, ${f_s} = T - {m_1}g\sin \theta $
$T$is the tension of the string.
${m_1}g\sin \theta $ is the sine component of the weight of mass ${m_1}$
${f_s} = \mu N$ $\mu $is the static coefficient of friction.
The normal force, $N = {m_1}g\cos \theta $
$T = {m_2}g$


Complete step-by-step solution:
The diagram in the problem is given by,

First, the diagram has to be modified by showing the components of the forces acting on the two masses ${m_1}$and ${m_2}$ .

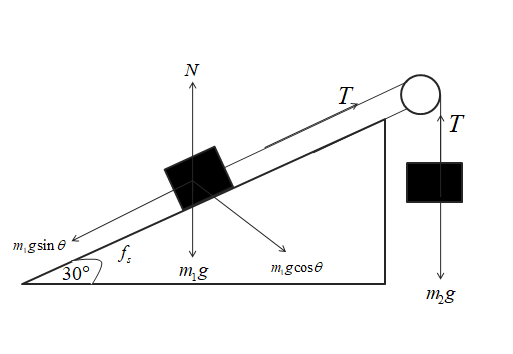
The weight of the mass ${m_1}$is ${m_1}g$ . It is divided into two components horizontal and vertical at an angle $\theta ( = 30^\circ )$ i.e. ${m_1}g\cos \theta $ and ${m_1}g\sin \theta $.
The tension of the string is $T$.
Now, The static frictional force, ${f_s} = T - {m_1}g\sin \theta $
From the diagram, it is shown that $T = {m_2}g$
$ \Rightarrow {f_s} = {m_2}g - {m_1}g\sin \theta $
Now, the formula of the static frictional force in terms of the static coefficient of friction $\mu $,
${f_s} = \mu N$
The normal force, $N = {m_1}g\cos \theta $
Now put the values of ${f_s}$ and $N$, we get
$ \Rightarrow \mu N = {m_2}g - {m_1}g\sin \theta $
$ \Rightarrow \mu {m_1}g\cos \theta = {m_2}g - {m_1}g\sin \theta $
$ \Rightarrow \mu {m_1}\cos \theta = {m_2} - {m_1}\sin \theta $
$ \Rightarrow \mu = \dfrac{{{m_2} - {m_1}\sin \theta }}{{{m_1}\cos \theta }}$
Given that, ${m_1} = 100kg$
${m_2} = 80kg$
$\sin \theta = \sin 30 = 0.500$
$\cos \theta = \cos 30 = 0.866$
$ \Rightarrow \mu = \dfrac{{80 - \left( {100 \times 0.500} \right)}}{{\left( {100 \times 0.866} \right)}}$
$ \Rightarrow \mu = \dfrac{{80 - 50}}{{86.6}}$
$ \Rightarrow \mu = \dfrac{{30}}{{86.6}}$
$ \Rightarrow \mu = 0.346$
Hence the static coefficient of friction $ \Rightarrow \mu = 0.346$.

Note:The frictional force is the constraint to the motion of a body having motion relative to another. like gravitational force or electromagnetism, It is not a fundamental force. It is the force between two surfaces that are sliding, or going to slide, across each other. The direction of the frictional force is opposite to the direction of the surface.
There are two types of friction: 1. Static Friction is the highest force by a surface on a body until it remains stationary.
2. Sliding friction is the minimum force needed to keep the body having motion over a surface such that it moves similar distances in equal time.