Question

Drawing straight parallel lines to axes:
Draw the graph of $ x = 3 $

Answer 1

Hint: We know that the graph of a straight line depends upon the variable present in the given equation. If there is only one variable x present in equation then its graph will be parallel to y –axis, if there is only one variable y present in equation then graph will be parallel to x-axis and if there are both variables present in equation then graph of the equation will be slant line. Hence, from this we can say that the graph of the given equation will be a line parallel to y-axis.

Complete step-by-step answer:
The equation of a straight line is $ x = 3 $ .
As there is no y variable in the given equation. Therefore, I can say that the graph of $ x = 3 $ will not meet anywhere in the y-axis.
And so the graph of will be a vertical line parallel to the y-axis.
To plot its graph we can consider different values of y but keeping the value of x always 3.
Taking points $ (3,0),\,\left( {3,3} \right)\,\,and\,\,(3, - 1) $ .
Now, using these point let's draw graph of $ x = 3 $
First draw $ x{x^`} $ axis and $ y{y^`} $ axis as shown below:

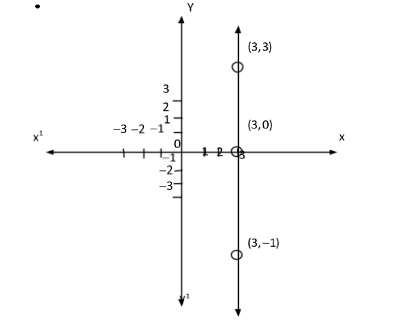
From the graph we came to know that $ x = 3 $ is a vertical line parallel to y-axis.
Hence, we conducted $ x = 3 $ graphically as a vertical line parallel to the y-axis.

Note: We know that a graph of a linear equation or a straight line is always a straight line. But there are three ways in which a graph of a line can be drawn. Graph of a line is either parallel to the x-axis, parallel to the y-axis or slant line. This we can easily judge from the given equation of line. If there is only one variable either x or y present in the equation, then the line will parallel to either x or y depending upon the given variable, otherwise the graph of line will be slant line.