Question

Draw, whenever possible, a rough sketch of:
A triangle with both the line and rotational symmetries of order more than 1.

Answer 1

Hint: In this question, we have to draw that triangle which should have both the line and rotational symmetries of order more than 1. It means that when it is rotated through \[{{360}^{o}}\], it should be the same as the original figure more than once during the rotation of the figure. Also there should be more than one axis line for the figure through which the figure is symmetric.

Complete step-by-step answer:
So the triangle with both the line and rotational symmetries of order more than 1 is an equilateral triangle.

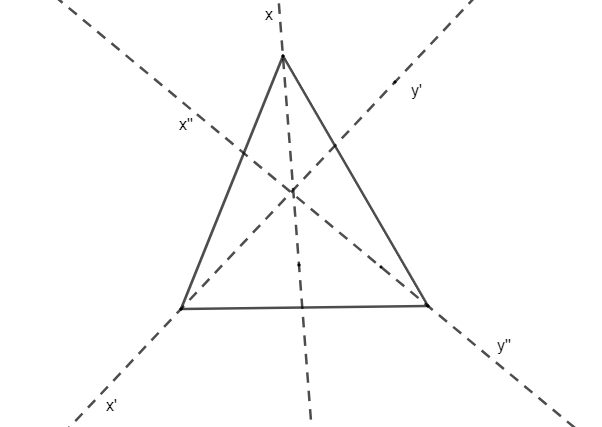
In the above equilateral triangle, there are three lines through which the equilateral triangle is symmetric with. These three lines indicate that the above triangle has order of line symmetry=3. This means that the condition for the line symmetry is satisfying. Also the equilateral triangle, when rotated through the angles of \[{{120}^{o}},{{240}^{o}}\]and\[{{360}^{o}}\], it appears to be same as the rotational figure, so we can say that it has rotational symmetry.
So we can say that an equilateral triangle has both line and rotational symmetry. Also, there are three lines of symmetry in the equilateral triangle, so its order is three. Also there are three angles at which the rotational symmetry of an equilateral triangle exists. So the order of rotational symmetry is 3.


Note: It is necessary that the triangle is equilateral to satisfy the condition of the question. If the triangle is isosceles, the condition of rotational and line symmetry does not exist. This case is the same with the scalene triangle also. So, due to above reasons, the triangle should be an equilateral triangle.