Question

Draw two concentric circles of radii $ 3cm $ and $ 5cm $ . Taking a point on outer circle constructs the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
 $
  A.\,\,3cm \\
  B.\,\,4cm \\
  C.\,\,5cm \\
  D.\,\,6cm \\
  $

Answer 1

Hint: Here first we will draw two concentric circles with center O and then from any point P from outer circle we first draw a pair of tangents to smaller circle. And then using Pythagoras theorem to find the actual length of the tangent.

Complete step-by-step answer:
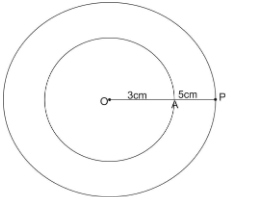
For this we first draw two concentric circles of radius $ 3cm\,\,and\,\,5cm $ having center (O). Where OA = $ 3cm $ and OP = $ 5cm $ .

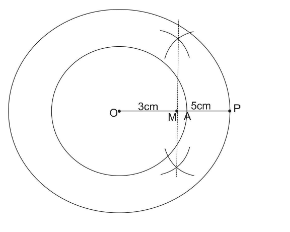
To draw a pair of tangents from P we first draw a perpendicular bisector of OP.
For this we put two arcs of radius greater than half of OP on both sides of line OP and name it as M where it meets line OP.

Now, draw an arc of radius OM, from M on a small circle, where these two arcs meet the circle and name them as A and B. Join A and B with P to have a pair of tangents on a small circle from point P.

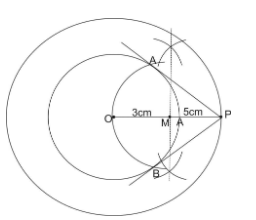
Which is the required construction of a pair of tangents from a point on the outer circle of two concentric circles.
Now, to measure the actual length of tangent.
We first join OA (radius of the circle) and then apply Pythagora's theorem. To find the length of AP. Which is given as:

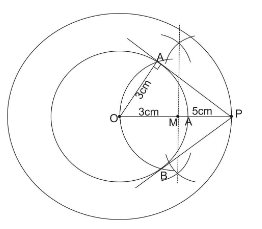
In triangle OAP, we have $ \angle A = {90^0} $ .
Therefore, $ {\left( {OP} \right)^2} = {(OA)^2} + {(AP)^2} $
Substituting values in above. We have,
 $
  {(5)^2} = {(3)^2} + {(AP)^2} \\
   \Rightarrow 25 = 9 + {(AP)^2} \\
   \Rightarrow 25 - 9 = {(AP)^2} \\
   \Rightarrow {(AP)^2} = 16 \\
   \Rightarrow AP = 4 \;
  $
Therefore, the length of tangents from P is $ 4cm $ .
Hence, from given four options correct option is (B)
So, the correct answer is “Option B”.

Note: Tangents and radius always make an angle of $ {90^0} $ . Therefore, a triangle formed by joining three points center, point of contact and from where tangents are drawn form a right angle triangle and hence using Pythagoras theorem we can find the length of the tangent when radius and distance between Center and point is given.