Question

Draw the Venn diagrams of the sets $ \left( {A - B} \right) $ and $ \left( {B - A} \right) $

Answer 1

Hint: Venn diagram is basically an illustration used to show the relation between two sets. It is a visual representation of the sets and is drawn using circles. In the given sets, $ A - B $ represents all the elements in A that are not present in B and the set $ B - A $ represents all elements in B that are not in A.

Complete step-by-step answer:
Given to us are two sets $ \left( {A - B} \right) $ and $ \left( {B - A} \right) $
Let us first draw the Venn diagram for the set $ \left( {A - B} \right) $
 $ \left( {A - B} \right) $ is a set of all elements present in A that are not elements of B. Let us draw the sets A and B first.

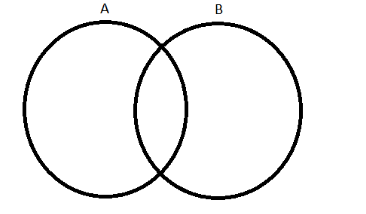
The above figure is a Venn diagram representation of the sets A and B. For the set $ \left( {A - B} \right) $ the region that contains the elements of A and also excludes the elements of B should be shaded. So the above Venn diagram now becomes:

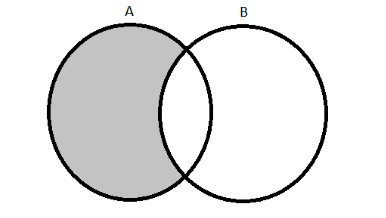
This above figure shows the Venn diagram of the set $ A - B $ .
Similarly, we can draw the Venn diagram of the set $ B - A $
The set $ B - A $ contains all the elements in B that are not in A. So in the Venn diagram we should only shade the region that has elements of B excluding all the elements of A.

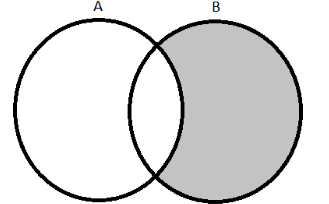
The above figure shows the Venn diagram of the set $ B - A $

Note: The set $ A - B $ can also be written as $ A - \left( {A \cap B} \right) $ . The set $ A \cap B $ contains all the elements that are common in between set A and set B. So in order to form the set $ A - B $ , the set of common terms of A and B are excluded from set A and vice-versa for set B.