Question

Draw the $v - t$ graph of uniform motion and the area under the $v - t$ graph gives the displacement of the particle in a given time.
(A) True.
(B) false.

Answer 1

Hint: The Velocity Time Graph denotes the velocity and time a plot between velocity of an object and the time taken by the object. It declares the motion of the object that moves in a Straight Line. If the acceleration of the object is positive, then the slope of the velocity time graph is positive; that is an upward sloping line.

Complete step by step answer:
The equations of motion of kinematics delineate that the general concept of the motion of an object which is as the position, velocity or the acceleration of an object at different times. The three equations of motion control the motion of an object in $1D$, $2D$ and $3D$. The extraction of the three equations of motion is one of the most important equations in determining the velocity, time and acceleration of the object.

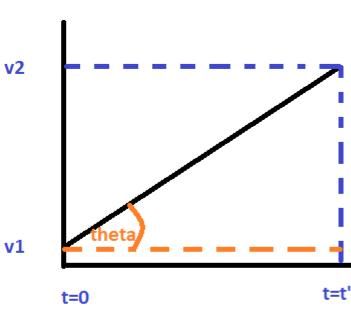
The area under the $v - t$ graph is equal to the area of the trapezium
Where, $v$ denotes the velocity and $t$ denotes the time taken.
That is;
$A = $ sum of parallel side of the trapezium x height of the trapezium /$2$.
$
 A = \dfrac{{\left( {u + v} \right) \times t}}{2} \\
\implies A = \dfrac{{\left( {u + v + at} \right) \times t}}{2} \\
\implies A = uv + \dfrac{1}{2} \times a{t^2} \\
\implies A = s \\
 $
Where, $A$ denote the area under the $v - t$ graph,$s$ denotes the distance of the trapezium, $u$ denotes the initial velocity, $v$ denotes the final velocity, $t$ denotes the time taken, $a$ denotes the acceleration.

So, the correct answer is “Option A”.

Note:
The velocity and the time graph show the changes in velocity of a moving object over particular given time. The slope of a velocity and time graph represents the acceleration of the moving object. The extraction of the three equations of motion is one of the most important equations in determining the velocity, time and acceleration of the object.