Question

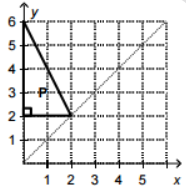
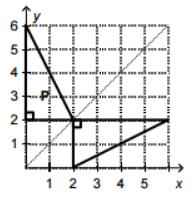
Draw the reflection image of triangle P using the dotted line as a line of symmetry.

A.

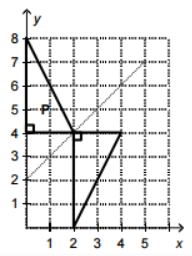
B.

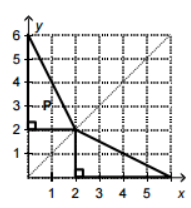
C.

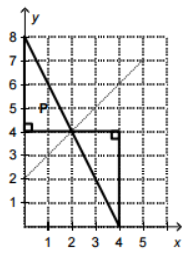
D.

Answer 1

Hint: In reflection, each point of a reflected image is at the same distance from the line of reflection. In order words, the distance of the corresponding points (original image and reflected image) is at the same distance from the line of reflection.

Complete step-by-step answer:
We know that, In reflection, each point of a reflected image is at the same distance from the line of reflection. In order words, the distance of the corresponding points (original image and reflected image) is at the same distance from the line of reflection.
From the given figure. Suppose the vertices of the triangle are \[A\left( {0,2} \right)\], \[B\left( {0,6} \right)\] and \[P\left( {2,2} \right)\].
Point P will be the same for both original image as well as reflected image, because the point P is on the line of reflection.
The reflection of the point \[A\left( {0,2} \right)\] will be \[A'\left( {4,2} \right)\], such that \[OA = OA'\].
Similarly, the reflection of the point \[B\left( {0,6} \right)\] will be \[B'\left( {4, - 2} \right)\], such that \[OB = OB'\].
From the given option, it can be observed that the option (C) shows the corresponding reflection of the point A, B and P.
Thus, the option (C) is the correct answer.

Note: In reflection, if a point lies over the line of reflection, there will be no change in the reflected point. In other words, the reflected point and original point will be the same, if the point lies over the line of reflection.