Question

How do you draw the Parabola \[y = 3x\left( {x + 2} \right)\]?

Answer 1

Hint: Here, we will first simplify the given equation of a Parabola. We will then compare it to the standard form of the parabola to find the coefficients. Then by using the \[x\]-coordinate of the vertex of the Parabola formula we will find the \[x\]-coordinate and by using the \[x\]- coordinate, we will find the \[y\]-coordinate of the vertex of the Parabola. We will substitute different values of \[x\] in the equation to find corresponding values of \[y\]. Thus we will find coordinate points and using these points we will draw the required graph of a parabola.

Formula Used:
The \[x\]-coordinate of the vertex of the Parabola is given by the formula \[h = \dfrac{{ - b}}{{2a}}\]

Complete Step by Step Solution:
The equation of Parabola is \[y = 3x\left( {x + 2} \right)\].
Now, we will multiply the terms using the distributive property, so we get
\[ \Rightarrow y = 3{x^2} + 6x\]…………………………………\[\left( 1 \right)\]
We can rewrite the above equation as
\[ \Rightarrow k = 3{h^2} + 6h\]……………………………………\[\left( 2 \right)\]
We know that the standard form of a Parabola \[y = a{x^2} + bx + c\] where the vertex of the parabola is at \[\left( {h,k} \right)\] which is similar to \[\left( {x,y} \right)\].
So, we get
\[\begin{array}{l}a = 3\\b = 6\\c = 0\end{array}\]
Now, by substituting the terms in the formula \[h = \dfrac{{ - b}}{{2a}}\], we get
\[h = \dfrac{{ - 6}}{{2\left( 3 \right)}} = \dfrac{{ - 6}}{6}\]
Dividing the terms, we get
\[ \Rightarrow h = - 1\]
Thus, the\[x\]-coordinate of the vertex of the Parabola is \[h = - 1\] .
Now, by substituting \[h = - 1\] in the equation \[\left( 2 \right)\], we get
\[ \Rightarrow k = 3{\left( { - 1} \right)^2} + 6\left( { - 1} \right)\]
\[ \Rightarrow k = 3 - 6\]
\[ \Rightarrow k = - 3\]
Therefore, the vertex of the Parabola is \[\left( { - 1, - 3} \right)\] .
Now, we will find the coordinates of the Parabola.
Substituting \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[y = 3{\left( 0 \right)^2} + 6\left( 0 \right)\]
Simplifying the expression, we get
\[ \Rightarrow y = 0\]
Substituting \[x = - 2\] in the equation\[\left( 1 \right)\], we get
\[y = 3{\left( { - 2} \right)^2} + 6\left( { - 2} \right)\]
Simplifying the expression, we get
\[ \Rightarrow y = 12 - 12\]
\[ \Rightarrow y = 0\]
Substituting \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[y = 3{\left( 1 \right)^2} + 6\left( 1 \right)\]
Simplifying the expression, we get
\[ \Rightarrow y = 3 + 6\]
\[ \Rightarrow y = 9\]
Substituting \[x = 2\] in the equation \[\left( 1 \right)\], we get
\[y = 3{\left( 2 \right)^2} + 6\left( 2 \right)\]
Simplifying the expression, we get
\[ \Rightarrow y = 12 + 12\]
\[ \Rightarrow y = 24\]

Therefore, the coordinates of the equation of line are \[\left( { - 2,0} \right)\] ,\[\left( { - 1, - 3} \right)\],\[\left( {0,0} \right)\], \[\left( {1,9} \right)\] and \[\left( {2,24} \right)\]

Now, we plot the graph for the co-ordinates, we get

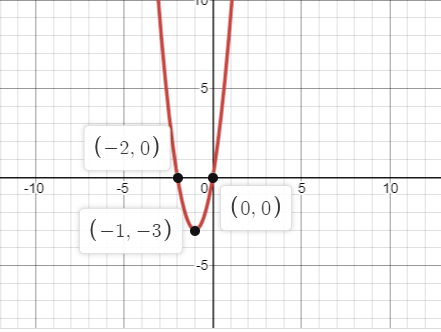
Note:
We know that the vertex of a Parabola is the minimum or maximum point of a Parabola. If \[a > 0\], then the vertex is the minimum point and the parabola will open upwards. If \[a < 0\], then the vertex is the maximum point and the parabola will open downwards. Therefore, the given equation’s vertex is the minimum point and the given equation of Parabola will open upwards. Vertex is the major part of drawing a Graph of the equation of the Parabola.