Question

Draw the graphs of $x=0,y=0\And x+y=2$. Shade region enclosed and write the name of the figure formed. Find its area and perimeter.

Answer 1

Hint: First of all draw the lines given in question on the graph paper. After drawing the three lines on the graph you will find that the area enclosed by these lines is a triangle so find the area of the triangle by using the formula for area of triangle which is equal to $\dfrac{1}{2}\left( base \right)\left( height \right)$.

Complete step by step solution:
The straight lines given in the question are:
 $x=0,y=0\text{ and }x+y=2$
The line $x=0$ is the y – axis, the line $y=0$ is the x – axis and to draw the line $x+y=2$ put $x=0$ in this equation you will get $y=2$ and substituting $y=0$ in the equation we get $x=2$. Using this information we can draw lines on the graph as follows:

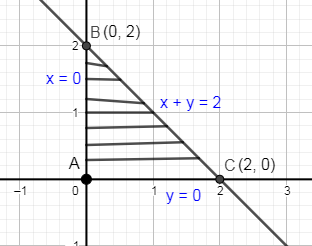
In the above figure, we have shaded the region enclosed by $x=0,y=0\And x+y=2$ which we have shown by ABC. The shaded region is forming a triangle and we have to find the area of the shaded region so we are going to find the area of triangle ABC.
 Area of triangle = $\dfrac{1}{2}\left( base \right)\left( height \right)$
Now, in the triangle ABC, the base is AC and the height is BA. From the above figure, the length of AC is equal to 2 and the length of BA is equal to 2. Substituting these values of base and height in the above equation we get,
Area of $\Delta ABC$ $=\dfrac{1}{2}\left( base \right)\left( height \right)$
Area of $\Delta ABC$ $=\dfrac{1}{2}\left( 2 \right)\left( 2 \right)$
In the above equation, 2 will be cancelled out from the numerator and denominator on the right hand side of the equation.
Area of $\Delta ABC$ $=2\text{ sq}\text{. units}$
We are also asked to find the perimeter of the triangle. We know that perimeter means the sum of the lengths of the boundaries of the figure so perimeter is the sum of all the sides of the triangle ABC.
As $\Delta ABC$ is right angled triangle, right angled at A so BC is the hypotenuse and applying Pythagoras theorem we get,
${{\left( BC \right)}^{2}}={{\left( BA \right)}^{2}}+{{\left( AC \right)}^{2}}$
Substituting BA and AC as 2 in the above equation we get,
$\begin{align}
  & {{\left( BC \right)}^{2}}=4+4 \\
 & {{\left( BC \right)}^{2}}=8 \\
\end{align}$
Taking square root on both the sides we get,
$BC=2\sqrt{2}$
Now, the perimeter of $\Delta ABC$ is equal to the sum of the sides BA, AC and BC.
BA + AC +BC
$\begin{align}
  & =2+2+2\sqrt{2} \\
 & =2\left( 2+\sqrt{2} \right) \\
\end{align}$
Hence, the area of the shaded region is 2 sq. units and the perimeter of the shaded region is $2\left( 2+\sqrt{2} \right)$.

Note: You might be thinking that when taking the square root of BC in the above solution we have only taken the positive value i.e. $2\sqrt{2}$ not the negative value i.e. $-2\sqrt{2}$. The reason behind is that the length of the side cannot be negative. You have also seen that we cannot say -2 metres length of cloth. We always deal lengths with the positive value.