Question

Draw the graphs of the following equations:
$\begin{align}
  & 2x-3y+6=0 \\
 & 2x+3y-18=0 \\
 & y-2=0 \\
\end{align}$
Find the vertices of the triangle so obtained. Also, find the area of the triangle.

Answer 1

Hint: Here, first we have to draw the graph of three equations separately by finding two points through which the line passes. Next, find the point of intersection of lines of all three equations. Our required portion will be a triangle $\Delta ABC$, and the point of intersections are the vertices of the triangle. Finally, find the area of the triangle by applying the formula:
$A=\dfrac{1}{2}\times Base\times Height$ where A is the area of the triangle.

Complete step-by-step answer:

Here, we are given with the equations:
$\begin{align}
  & 2x-3y+6=0 \\
 & 2x+3y-18=0 \\
 & y-2=0 \\
\end{align}$
Now, we have to draw the graph of the above equations. Then, we have to find the vertices of the triangle so obtained. We also have to find the area of the triangle.
First consider the equation:
$2x-3y+6=0$
Now, we have to draw the line corresponding to the given equation. For that consider two points.
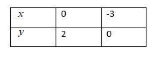
When $x=0$ we have:
$\begin{align}
  & 2\times 0-3y+6=0 \\
 & \Rightarrow -3y+6=0 \\
\end{align}$
Now, take 6 to the right side, 6 becomes -6, we get:
$-3y=-6$
Next, by cross multiplication, we obtain:
$y=\dfrac{-6}{-3}$
Now, by cancellation we get:
$y=2$
Now, consider the equation $2x-3y+6=0$ when $y=0$,
$\begin{align}
  & \Rightarrow 2x-3\times 0+6=0 \\
 & \Rightarrow 2x+6=0 \\
\end{align}$
Next, by taking 6 to the right side we get:
$2x=-6$
In the next step by cross multiplication we get:
$x=\dfrac{-6}{2}$
$\Rightarrow x=-3$

Next, consider the equation:
$2x+3y-18=0$
Now, we have to find two points to draw the graph of the equation.
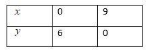
For that take $x=0$,
$\begin{align}
  & \Rightarrow 2\times 0+3y-18=0 \\
 & \Rightarrow 3y-18=0 \\
\end{align}$
Next, take -18 to the right side and it becomes 18. Hence we will get:
$3y=18$
Now, by cross multiplication we get:
$\begin{align}
  & y=\dfrac{18}{3} \\
 & \Rightarrow y=6 \\
\end{align}$
Now, for $y=0$ we will obtain:
$\begin{align}
  & 2x+3\times 0-18=0 \\
 & \Rightarrow 2x-18=0 \\
\end{align}$
Next, by taking -18 to the right side it becomes 18. That is,
$\Rightarrow 2x=18$
Hence, by cross multiplication,
$\begin{align}
  & \Rightarrow x=\dfrac{18}{2} \\
 & \Rightarrow x=9 \\
\end{align}$
Therefore, the two points are:

Next, consider the equation $y-2=0$. By taking -2 to the right side,
$\Rightarrow y=2$
Now, we can find the intersecting points of the three equations:
Consider the equation:
$2x-3y+6=0$
Next, taking 6 to the right side,
$\Rightarrow 2x-3y=-6$
Now, consider the equation:
$2x+3y-18=0$
Next, take -18 to the right side,
$\Rightarrow 2x+3y=18$
So, we have the equations:
$\begin{align}
  & 2x-3y=-6 \\
 & 2x+3y=18 \\
\end{align}$
Now, by adding the above equations,
$\Rightarrow 4x=12$
Next, by cross multiplying,
$\begin{align}
  & \Rightarrow x=\dfrac{12}{4} \\
 & \Rightarrow x=3 \\
\end{align}$
Now, substituting $x=3$ in $2x-3y+6=0$,
$\begin{align}
  & \Rightarrow 2\times 3-3y+6=0 \\
 & \Rightarrow 6-3y+6=0 \\
 & \Rightarrow 12-3y=0 \\
\end{align}$
In the next step, take 12 to the right side,
$\Rightarrow -3y=-12$
By cross multiplying,
$\begin{align}
  & \Rightarrow y=\dfrac{-12}{-3} \\
 & \Rightarrow y=4 \\
\end{align}$
Therefore, the intersecting point of the equations is (3, 4).
Now let us find the intersecting point of the equations:
$\begin{align}
  & 2x-3y+6=0 \\
 & 2x+3y-18=0 \\
 & y-2=0 \\
\end{align}$
Now, consider $y-2=0$,
$\Rightarrow y=2$
Next, substitute, $y=2$ in $2x+3y-18=0$,
$\begin{align}
  & \Rightarrow 2x+3\times 2-18=0 \\
 & \Rightarrow 2x+6-18=0 \\
 & \Rightarrow 2x-12=0 \\
 & \Rightarrow 2x=12 \\
 & \Rightarrow x=\dfrac{12}{2} \\
 & \Rightarrow x=6 \\
\end{align}$
Therefore, the intersecting point is (6, 2).
Now, we can find the intersecting point of the equations:
$\begin{align}
  & 2x-3y+6=0 \\
 & y-2=0 \\
\end{align}$
Now, $y-2=0$,
$\Rightarrow y=2$
We can substitute $y=2$ in $2x-3y+6=0$which,
$\begin{align}
  & \Rightarrow 2x-3\times 2+6=0 \\
 & \Rightarrow 2x-6+6=0 \\
 & \Rightarrow 2x+0=0 \\
 & \Rightarrow 2x=0 \\
 & \Rightarrow x=\dfrac{0}{2} \\
 & \Rightarrow x=0 \\
\end{align}$
Therefore, the intersecting point, (0, 2).
Now, with the help of points obtained by the three equations, we can construct the graph.
The graph is as follows:

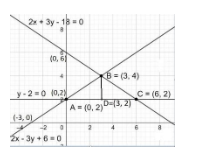
Here, from the graph we can say the intersections of all three equations will yield to the triangle $\Delta ABC$ with vertices A (0, 2), B (3, 4) and C (6, 2).
Now, we have to find the area of the $\Delta ABC$.
 We know that the area of the triangle, ‘A’ is defined by the formula:
$A=\dfrac{1}{2}\times Base\times Height$
Here, the base is AC and height is BD.
Now, we have to find AC and BD.
Next, from the figure we can say that AC is the length of x- axis from A to C which is:
AC = 6 – 0 = 6
BD is the length of y-axis from B to D which is:
 BD = 4 - 2 = 2
Therefore, the area of the triangle will be:
$\begin{align}
  & A=\dfrac{1}{2}\times AC\times BD \\
 & \Rightarrow A=\dfrac{1}{2}\times 6\times 2 \\
 & \Rightarrow A=\dfrac{1}{2}\times 12 \\
 & \Rightarrow A=6 \\
\end{align}$
Hence, we can say that the area of the triangle $\Delta ABC$ is 6 square units.

Note: Here, while finding the points through which the line passes we can also take the two equations and can equate one in terms of the other. Hence, the region common to all these equations will be a triangle, the points so obtained will be the vertices of the triangle. These points are required to find the area of the triangle.