Question

Draw the graphs of linear equations $ y = x $ and $ y = - x $ on the same cartesian plane. What do you observe?
A.Graph of each equation is a line passing through $ \left( {1,1} \right) $ .
B.Graph of each equation is a line passing through $ \left( {0,1} \right) $ .
C.Graph of each equation is a line passing through $ \left( {0,0} \right) $ .
D.Graph of each equation is a line passing through $ \left( {1,0} \right) $ .

Answer 1

Hint: Plot the graph of both the equations in the Cartesian plane (the plane having four quadrants) and then check the common point of the both equations.

Complete step-by-step answer:
The given equations of the line are: $ y = x $ and $ y = - x $
First we will take the equation $ y = x $ of the line.
Taking the values of x as 0, 1, 2 and 3 then we will get the values of y as 0, 1, 2 and 3. Hence the line of given equation is passing through the coordinates $ \left( {0,0} \right),\left( {1,1} \right),\left( {2,2} \right) $ and $ \left( {3,3} \right) $ of the plane and all the coordinated lies in the first quadrant of the plane.

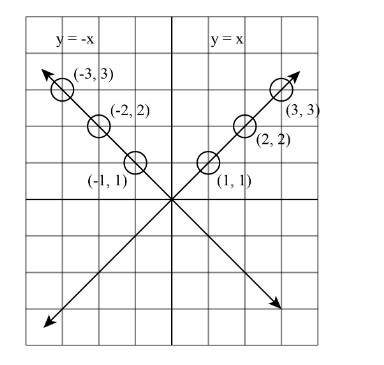
Now we will take the second equation $ y = - x $
Again we will take the values of x as 0, -1, -2 and -3 then we will get the values of y as 0, 1, 2 and 3. Hence the line of equation is passing through the coordinates $ \left( {0,0} \right),\left( { - 1,1} \right),\left( { - 2,2} \right) $ and $ \left( { - 3,3} \right) $ of the plane and all the coordinated lies in the second quadrant of the plane.
We will observe that they have one common point where the graph of both equations intersect is $ \left( {0,0} \right) $ .
So, the correct answer is “Option C”.

Note: Take the point and solve the equation correctly. It can also be carried by using the quadrant, the equation $ y = x $ has its all values in the first quadrant and the equation $ y = - x $ has all its values in the second quadrant. It means they have no common point between them except origin as they both start from the same point.