Question

Draw the graph of $ y={{x}^{2}}-x-2 $ and find its roots

Answer 1

Hint: Try to manipulate into any of known conics. First factorize the equation. Find the roots of the equation. Now by using the equation in form of any conic ty to draw the graph. Make all the points which are needed to describe the graph. This graph and roots are required results.

Complete step-by-step answer:
Given equation in the question is written in the form of:
 $ y={{x}^{2}}-x-2 $
To Find its roots we must equate it to 0, we get:
 $ {{x}^{2}}-x-2 $
By comparing it to equation given by \[a{{x}^{2}}+bx+c\], we get the following:
The value of the variable a is given by 1.
The value of the variable b is given by -1.
The value of the variable C is given by -2.
The product \[a\times c\] can be found by multiplying a,c we get:
\[a\times c\text{ }=1\times \left( -2 \right)\]
 By simplifying the above equation, we get the product as:
 \[a\times c=-2\]
The two numbers whose product is -2, sum is b= -1 are -2,1
So, by writing -x as x-2x we get the quadratic as:
 $ {{x}^{2}}-2x+x-2=0 $
By taking x common from first two terms, we get it as:
 $ x(x-2)+x-2=0 $
By taking 1 common from last two tums, we get it as:
 $ x(x-2)+1(x-2)=0 $
By taking $ (x-2) $ common from whole equation, we get it as:
 $ (x-2)(x+1)=0 $
By above equation, we can write the roots of equation:
 $ x=-1,2 $
By this we can say that curve passes through points:
(-1,0) (2,0)
If we substitute x=0, we can derive y intercept of graph
By substituting x=0, we get the equation of y as:
\[y=0-0-2\]
By simplifying the equation, we can write it in form of:
\[y=-2\]
By this we can say it also passes through the point:
(0-2).
As it is a quadratic in x, we can say the graph is a type of parabola facing the y-axis. with the 3 points we drawn it as:

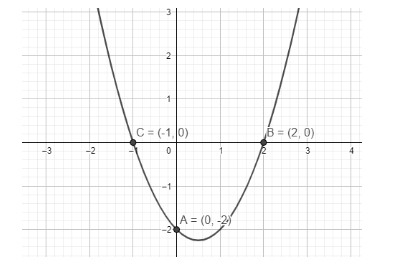
Therefore this is a graph of a given equation.


Note: Be careful while factorizing the equation. Find the product \[a\times c\] with the sign, because if the sign changes the roots will change. Alternate method is to convert it into $ {{x}^{2}}=4ay $ form to find vertex and then plot the graph. You can get roots from the graph itself.