Question

Draw the graph of $y = {x^2}$ and $y = x + 2$ and hence solve the equation ${x^2} - x - 2 = 0$.

Answer 1

Hint: The solution of the given equation can be found out by the point of intersection of the given parabola and the given line. We will draw the graph and proceed further.

Complete step-by-step answer:

Let us first draw the graph of line and parabola and then we will see the point of their intersection to find the solution of the given equation.

For the parabola $y = {x^2}$ and the line $y = x + 2$ we have the graph as follows.

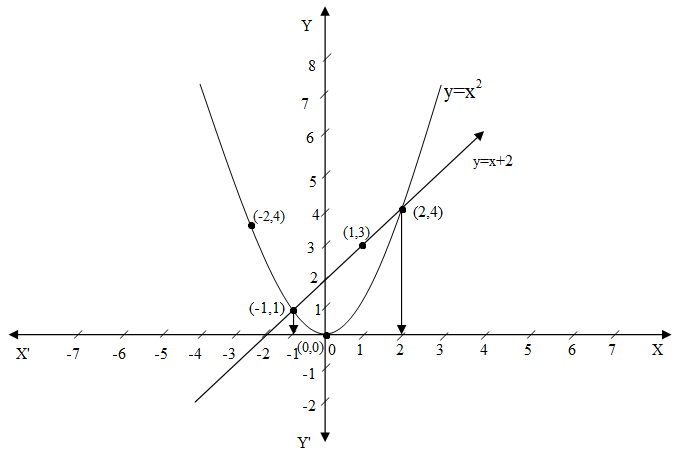
The graphs of the parabola $y = {x^2}$ and the line $y = x + 2$ intersects at the points $\left( {2,4} \right)\& \left( { - 1,1} \right)$.
As the x coordinates for both of the points are -1 and 2.
Hence, the roots of the quadratic equation ${x^2} - x - 2 = 0$ are -1 and 2.

Note: This problem, if not mentioned specifically to solve by the graphical method, can be solved directly by substituting the value of any of the variables from equation to another. And finally solving for the roots of the quadratic equation. In order to solve such problems students must remember the methods to draw the curves by finding random points.