Question

Draw the graph of y = ${x^2}$ + 2x – 3 and hence find the roots of ${x^2} - x - 6 = 0$.

Answer 1

Hint – In this question first convert the equation into the standard form and check whether the form is parabola, hyperbola, ellipse or a circle, after identifying find out the intersection points of the curve with the coordinate axes and plot the graph so use these concepts to reach the solution of the question.

Complete step-by-step answer:

Given equation of the graph is
Y = ${x^2}$ + 2x – 3
Now make the complete square in x by adding and subtracting by half the square of the coefficient of x in R.H.S so we have,
Half the square of the coefficient of x is ${\left( {\dfrac{2}{2}} \right)^2}$= ${1^2} = 1$
So add and subtract by this in R.H.S of the above equation we have,
 Y = ${x^2}$ + 2x – 3 + 1 – 1
Now simplify this we have,
Y = ${x^2}$ + 2x + 1 – 4
$ \Rightarrow y = {\left( {x + 1} \right)^2} - 4$
Now take 4 to L.H.S we have,
$ \Rightarrow y + 4 = {\left( {x + 1} \right)^2}$
$ \Rightarrow {\left( {x + 1} \right)^2} = 1\left( {y + 4} \right)$
So as we know this is the equation of the parabola.
Now the standard equation of the parabola is given as ${X^2} = 4aY$, where 4a is the length of the latus rectum.
The vertex of the parabola is X = 0 and Y = 0 i.e. (0, 0).
So on comparing X = x + 1 = 0 and Y = y + 4 = 0
So on solving, x = -1 and y = -4
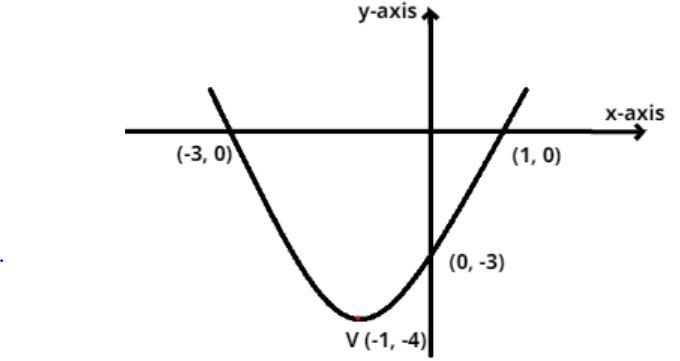
So the vertex of the parabola is (-1, -4)
Now find out the intersection point of this parabola with the coordinate axes.
Now the intersection point of this parabola with the x-axis is by putting y = 0 in the equation of the parabola so we have,
$ \Rightarrow {\left( {x + 1} \right)^2} = 1\left( {0 + 4} \right) = 4$
Now take square root on the both sides we have,
$ \Rightarrow \left( {x + 1} \right) = \sqrt 4 = \pm 2$
Now when, x + 1 = 2 therefore, x = 1
And when, x + 1 = -2 therefore, x = -3
So the intersection point of the parabola with the coordinate axis is (1, 0) and (-3, 0) as shown in the figure.
Now the intersection point of this parabola with the y-axis by putting x = 0 in the equation of the parabola so we have,
$ \Rightarrow {\left( {0 + 1} \right)^2} = 1\left( {y + 4} \right)$
$ \Rightarrow 1 = y + 4$
$ \Rightarrow y = 1 - 4 = - 3$
So the intersection point of the parabola with the coordinate axis is (0, -3) as shown in the figure.
So this is the required graph of the given curve.
Now we have to find the roots of the equation ${x^2} - x - 6 = 0$
So factorize this equation we have,
$ \Rightarrow {x^2} - 3x + 2x - 6 = 0$
Now simplify it we have,
$ \Rightarrow x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0$
$ \Rightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0$
$ \Rightarrow x = 3, - 2$
So this is the required roots of the given equation.
So these are the required answers.

Note – Whenever we face such types of questions the key concept we have to remember is that to make a complete square in any variable we have to add and subtract the square of the coefficient of the single degree variable, then convert the equation into the standard form of the parabola and compare it with the standard equation of the parabola as above, then find out the intersection point of this parabola with the x-axis is by putting y = 0 and the intersection point of this parabola with the y-axis is by putting x = 0 then mark all these points and plot the graph.