Question

How do you draw the graph of $ y = {\left( {x - 4} \right)^2} $ by plotting the points ?

Answer 1

Hint: We are required to draw the graph of the function given to us, $ y = {\left( {x - 4} \right)^2} $ . Hence, we first have to find the nature of the curve that the given equation represents and then find the center or the vertex of the conic. Then, we draw the graph of the function keeping in mind the graphical transformations and the necessary graphing tools.

Complete step-by-step answer:
In this question, we are required to draw the graph of the function $ y = {\left( {x - 4} \right)^2} $ . This function has to be first converted into the standard form. Then, we find out the nature of the curve that the given equation represents.
So, $ y = {\left( {x - 4} \right)^2} $
Opening up the whole square, we get,
 $ \Rightarrow y = \left( {{x^2} - 8x + 16} \right) $
So, we can clearly see that the given equation represents a translated parabola of form $ y = {\left( {x - \alpha } \right)^2} $ where $ \left( {\alpha ,0} \right) $ is the vertex of the parabola. Hence, it is an upward facing parabola. Now, comparing $ y = {\left( {x - 4} \right)^2} $ with general form of equation of parabola facing upwards, $ \left( {y - \beta } \right) = {\left( {x - \alpha } \right)^2} $ , where $ \left( {\alpha ,\beta } \right) $ is the vertex of the parabola, we get, $ \alpha = 4 $ and $ \beta = 0 $ .
So, we get the coordinates of the vertex of the parabola as $ (4,0) $ .
Similarly, we put values of x as $ 2 $ and $ 3 $ into the equation so as to obtain the value of y.
Putting x as $ 2 $ , we get,
 $ \Rightarrow y = {\left( {2 - 4} \right)^2} $
 $ \Rightarrow y = {\left( { - 2} \right)^2} $
 $ \Rightarrow y = 4 $
Putting x as $ 3 $ , we get,
 $ \Rightarrow y = {\left( {3 - 4} \right)^2} $
 $ \Rightarrow y = {\left( { - 1} \right)^2} $
 $ \Rightarrow y = 1 $
Plotting the graph of the equation, we get,

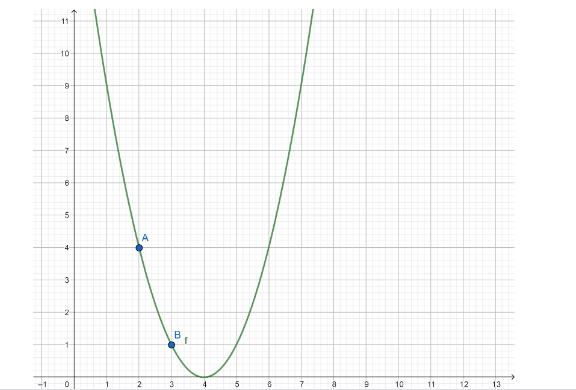
Note: To draw the graph of a function, we either need the points that lie on the graph of the function when plotted on graph paper or the equation of the function. In the given question, we are given an equation of parabola to plot on the graph that can be plotted easily once we get to know the vertex and focus of the parabola.