Question

Draw the graph of $xy\ \ =\ \ 20$ where $ x , y > 0 $. Use the graph to find ${{y}_{1}}$ when $x\ =\ 5$ , and to find ${{x}_{1}}$ when $y\ =\ 10$ . Then find ${{x}_{1}}\ +\ {{y}_{1}}$ .\[\]

Answer 1

Hint: We see that the given equation of curve is in implicit form $xy\ \ =\ \ 20$ we write it in the explicit form of function $y=f\left( x \right)=\dfrac{20}{x}$. We assume 3 positive values and 3 negative values for $x$. We find the corresponding functional values. $y=f\left( x \right)$ We find the coordinates of points $\left( x,f\left( x \right) \right)$ and join them to get the plot of the curve . We draw the lines $x\ =\ 5$ and the ordinate of its point of intersection with the curve $xy\ \ =\ \ 20$ will be ${{y}_{1}}$. We draw the lines $y\ =\ 10$ and abscissa of its point of intersection with the curve $xy\ \ =\ \ 20$ will be ${{x}_{1}}$. \[\]

Complete step-by-step answer:
We have the given equation of the curve in the question as
\[xy\ \ =\ \ 20\]
Here the condition is the non-negative constraints $ x , y > 0 $ which means the curve is only in first quadrant. We see that it is in implicit form which means it is not expressed in the form $y=f\left( x \right)$. We write explicitly in the form $y=f\left( x \right)$ as
\[\begin{align}
  & xy=20 \\
 & \Rightarrow y=\dfrac{20}{x} \\
 & \Rightarrow y=f\left( x \right)=\dfrac{20}{x}....\left( 1 \right) \\
\end{align}\]
We can see that above function is clearly not defined for $x=0$ We see that $x$ and $y$ are multiplied to each other and the product is 20. We can take the factors of 20 as assumed integral values of $x$. We have the factors of 20 as 1,2,4,5,10,20. We take 5 values $x=1,2.5,4,8,20$ in equation and find the corresponding values of $y=f\left( x \right)=\dfrac{20}{x}$. We write the obtained values in the following table. \[\]
 

We plot the obtained points $\left( x,f\left( x \right) \right)$ and join the points to obtain the plot of the curve $xy=20$ with $x,y > 0 $\[\]

 

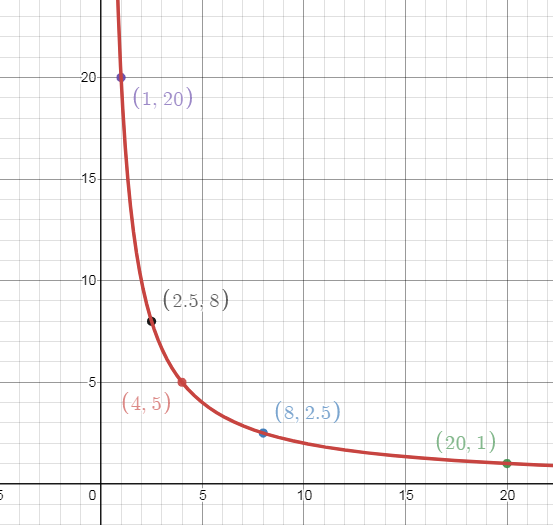
We are also asked to use the graph to find ${{y}_{1}}$ when $x=5$ , and to find ${{x}_{1}}$ when $y=10$ and then find ${{x}_{1}}+{{y}_{1}}$ . So we draw the lines $x=5$ and $y=10$ and then observe only the first quadrant as there are only positive values and see where the lines intersect the curve. \[\]

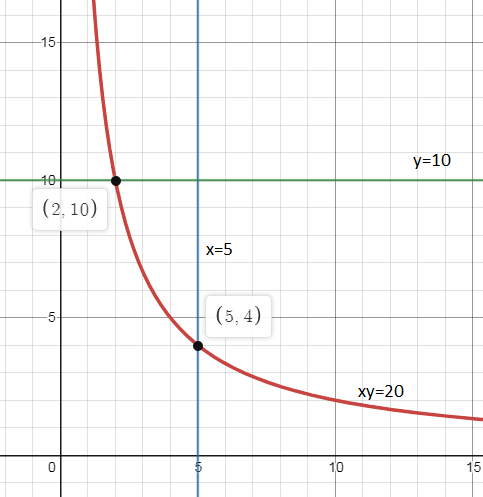
We observe that the line $x=4$ intersects the curve $xy=20$ at $\left( 5,4 \right)$, so when $x=4$ we have ${{y}_{1}}=4$. We also observe that the line $y=10$ intersects the curve at $\left( 2,10 \right)$, so when $y=10$ we have ${{x}_{1}}=2$. The required value from the question is ${{x}_{1}}+{{y}_{1}}=2+4=6$.\[\]

Note: We can verify the points of intersection by putting them in the equation of the curve. The plot we obtained is the plot of a rectangular hyperbola whose standard equation is given by $XY=C$ for some real constant $C$. The rectangular hyperbola is special type of hyperbola obtained when we put the condition $a=b$ in the general equation of an hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.