Question

How do you draw the graph of $ {x^2} + {y^2} - 8x + 6y + 16 = 0 $ ?

Answer 1

Hint: We are required to draw the graph of the function given to us, $ {x^2} + {y^2} - 8x + 6y + 16 = 0 $ . Hence, we first have to find the nature of the curve that the given equation represents and then find the center or the vertex of the conic. Then, we draw the graph of the function keeping in mind the graphical transformations and the necessary graphing tools.

Complete step by step solution:
In this question, we are required to draw the graph of the function $ {x^2} + {y^2} - 8x + 6y + 16 = 0 $ .
The given equation represents a circle as there is on xy term in the equation and the coefficient of the terms $ {x^2} $ and $ {y^2} $ are equal and equal to one.
Now, we know that the standard equation of a circle is $ {(x - h)^2} + {(y - k)^2} = {r^2} $ . So, this function has to be first converted into the standard form. Then, we find out the nature of the curve that the given equation represents and draw the graph accordingly.
So, $ {x^2} + {y^2} - 8x + 6y + 16 = 0 $
Rearranging the terms and grouping the terms with x and y, we get,
 $ \Rightarrow \left( {{x^2} - 8x} \right) + \left( {{y^2} + 6y} \right) + 16 = 0 $
Adding and subtracting same terms from the expression, we get,
 $ \Rightarrow \left( {{x^2} - 8x + 16} \right) + \left( {{y^2} + 6y + 9} \right) + 16 - 16 - 9 = 0 $
Cancelling the terms same in magnitude and opposite in sign, we get,
 $ \Rightarrow \left( {{x^2} - 8x + 16} \right) + \left( {{y^2} + 6y + 9} \right) - 9 = 0 $
We know that $ {\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2} $ and $ {\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2} $
Now, forming whole square terms and simplifying calculations, we get,
 $ \Rightarrow {\left( {x - 4} \right)^2} + {\left( {y + 3} \right)^2} - 9 = 0 $
 $ \Rightarrow {\left( {x - 4} \right)^2} + {\left( {y + 3} \right)^2} = {3^2} $
Now, we can verify that the given equation is of a circle as it resembles the standard equation of a circle.
Now comparing with standard form of equation of circle $ {(x - h)^2} + {(y - k)^2} = {r^2} $ where the center of the circle is $ \left( {h,k} \right) $ and radius $ = r $ .
So, in the given equation, we get the coordinates of center $ = (4, - 3) $ and radius $ = 3 $ units.
Plotting the graph of the equation, we get,

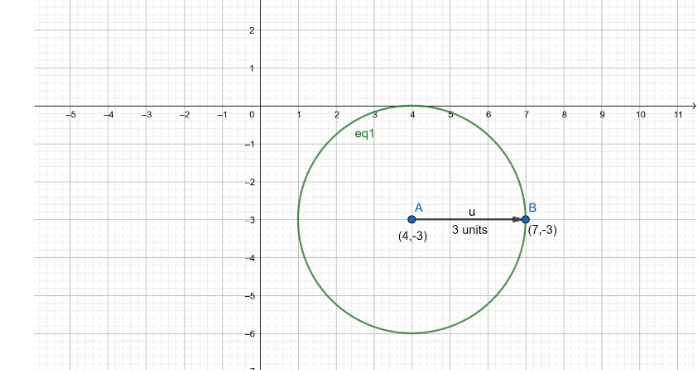
So, in the graph above, the point A with coordinates $ \left( {4, - 3} \right) $ is the center of the circle and point B with coordinates $ \left( {7, - 3} \right) $ is a point lying on the circle. The vector u is the radius vector of the circle whose magnitude is $ 3 $ as the radius of the circle is $ 3 $ units. Also, the eq1 represents the graph of the equation of the circle given to us.

Note: We can also solve the given problem by comparing the given equation $ {x^2} + {y^2} - 8x + 6y + 16 = 0 $ with the general equation of the circle $ {x^2} + {y^2} + 2gx + 2fy + c = 0 $ . So, we get the value of g as $ \left( { - 4} \right) $ , value of f as $ 3 $ , and value of c as $ 16 $ . We know that the coordinates of the center of the circle are $ \left( { - g, - f} \right) $ . So, we get the coordinates of the circle as $ \left( {4, - 3} \right) $ . Also, the radius of the circle can be calculated as $ \sqrt {{f^2} + {g^2} - c} $ . So, we get the radius as $ \sqrt {{{\left( 3 \right)}^2} + {{\left( { - 4} \right)}^2} - 16} = 3 $ units.