Question

Draw the graph of \[x + 5 = 0\].

Answer 1

Hint: The given equation represents a straight line and is in the form of \[x = - k\], and by the equation we can say that it is parallel to \[y\]-axis when the given equation is represented in a Cartesian plane, and by the equation it is clear that it passes through the point \[\left( { - 5,0} \right)\], so the graph is straight line which is parallel to \[y\]-axis, and passes through the point \[\left( { - 5,0} \right)\], that will be represented in the graph.

Complete step-by-step answer:
Given equation is \[x + 5 = 0\],
This can be rewritten as, \[x = - 5\],
Now firstly we will find the equation of the line that is parallel to the \[y\]-axis,
We know that the general form of equation of line will be,
\[y = mx + c\],
And the slope of the line parallel to \[y\]-axis is equal to the slope of the \[y\]-axis which is equal to infinity, i.e.,\[\dfrac{1}{0} = \infty \],
Now substituting the slope value we get,
\[y = \dfrac{1}{0} \cdot x + c\],
Now taking c to other side we get,
\[y - c = \dfrac{1}{0} \cdot x\],
Now cross multiplying we get,
\[\left( 0 \right)y - c = x\]
So, the equation of the line parallel to \[y\]-axis will be \[x = 0\],
Now the general equation of line parallel to \[y\]-axis will become \[x = k\], where \[k\] is constant as 0 is also a constant.
So from the above derivation, the given equation \[x = - 5\] is a line parallel to y-axis, and also we know that the line passed through the point \[\left( { - 5,0} \right)\],
Now representing the above equation on then graph we get,

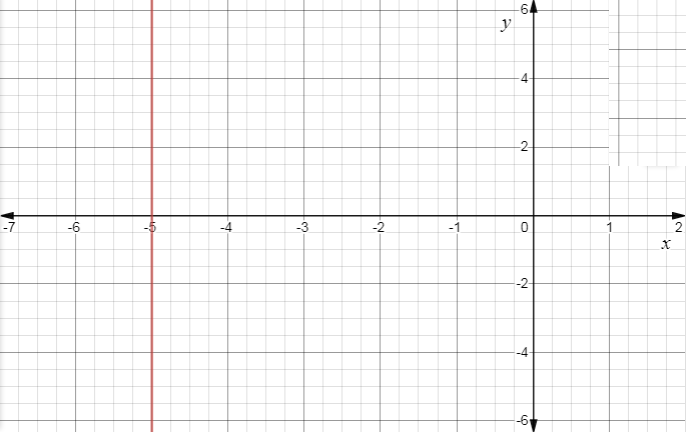
From the graph we can see that the line is parallel to \[y\]-axis and it passes through the point \[\left( { - 5,0} \right)\].

Note:
In these type of questions, that shows that line is parallel to \[x\]-axis and \[y\]-axis we must use slope intercept formula i.e., \[y = mx + c\], where m is the slope and c is the \[y\]-intercept of the line, and the graphs are usually represented on a Cartesian plane.