Question

Draw the graph of the polynomial \[f\left( x \right)={{x}^{3}}.\]

Answer 1

Hint: Assume f(x) = y and equate it with \[f\left( x \right)={{x}^{3}}.\] Now, substitute x = 0 to find the points at which the curve intersects the y-axis. Similarly, substitute y = 0 to find the points at which the curve intersects x – axis. Now, differentiate \[y={{x}^{3}}\] with respect to x and check if the function is increasing or decreasing. If \[\dfrac{dy}{dx}>0\] then it is increasing and if \[\dfrac{dy}{dx}<0\] then it is decreasing. Draw the curve with a free hand.

Complete step by step answer:
Here, we have been provided with the function \[f\left( x \right)={{x}^{3}}\] and we have been asked to draw its graph. Now, to draw the graph, we must know the points at which the curve intersects the coordinate axes if the function is increasing or decreasing. So, let us know these things about the given polynomial \[f\left( x \right)={{x}^{3}}.\] Here, we are assuming f(x) = y, so that the given polynomial becomes \[y={{x}^{3}}.\] To determine the point of intersection of the curves, we need to substitute x = 0 and y = 0 in the given equation one by one. So, we have,
(i) For x = 0, \[y={{0}^{3}}=0.\]
So, the curve intersects the y – axis at the origin (0, 0).
(ii) For y = 0, \[{{x}^{3}}=0,x=0.\]
So, the curve intersects the x – axis at the origin (0, 0).
Therefore, we can say that the curve \[y={{x}^{3}}\] intersects the axes at the origin only.
Now, differentiating \[y={{x}^{3}}\] with respect to x, we get,
\[\Rightarrow \dfrac{dy}{dx}=3{{x}^{2}}\]
Clearly, we can see that \[3{{x}^{2}}\] will be positive for all real values of x. So, we have,
\[\Rightarrow 3{{x}^{2}}>0\]
\[\Rightarrow \dfrac{dy}{dx}>0\]
Hence, the slope of the curve at any point will be positive.
Now, we can see that the range of the function \[f\left( x \right)={{x}^{3}}\] can be \[\left[ -\infty ,\infty \right].\] If we will substitute \[x=-\infty \] then \[f\left( x \right)=-\infty \] and if we substitute \[x=\infty \] then \[f\left( x \right)=\infty .\] So, the curve can be drawn as

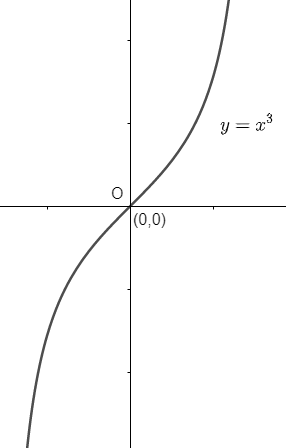
Note: One may note that we cannot find the values of maxima and minima of the given equation with the help of the second derivative test because the function is extending from \[-\infty \] to \[\infty .\] Always remember the basic rules to draw a graph of a given function. First determine the points of intersection, the sign of \[\dfrac{dy}{dx}\] and then determine the maxima and minima if possible.