Question

Draw the graph of the polynomial $f\left( x \right)={{x}^{2}}-2x-8$.

Answer 1

Hint: We will first start by using the fact that the graph of a standard quadratic equation like $a{{x}^{2}}+bx+c=0$ where a > 0 is concave upwards. Then we will use differential calculus to find the point of minima and finally we will draw the graph of ${{x}^{2}}-2x-8$.

Complete step-by-step answer:
Now, we have to draw the graph of $f\left( x \right)={{x}^{2}}-2x-8$.
Now, we know that the graph of a quadratic function $f\left( x \right)=a{{x}^{2}}+bx+c=0$ where a > 0 is,

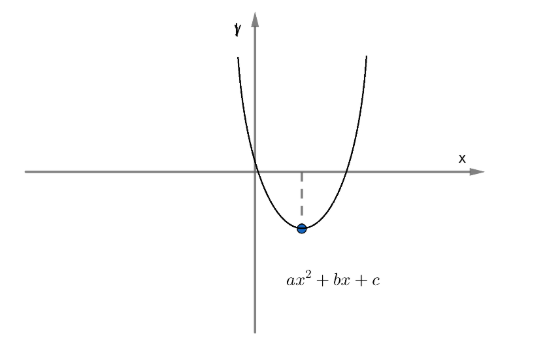
Now, we have the function as $f\left( x \right)={{x}^{2}}-2x-8$.
Now, we know that the curve will be concave upwards as a > 0, but we have to find its point of minima and its intercept at the x, y axis to draw the graph more precisely.
Now, we know that for points of minima we have to find the critical points at which $\dfrac{d}{dx}\left( f\left( x \right) \right)=0$. So, we have,
$\dfrac{d}{dx}\left( {{x}^{2}}-2x-8 \right)=0$
Now, we know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$.
$\begin{align}
  & \Rightarrow 2x-2=0 \\
 & x=\dfrac{2}{2} \\
 & x=1 \\
\end{align}$
So, point of minima is x = 1.
Now, we have for $x=0,y=-8$ and now we will plot both these points on the graph and join it as per our standard result. So, we have the graph of ${{x}^{2}}-2x-8$ as,

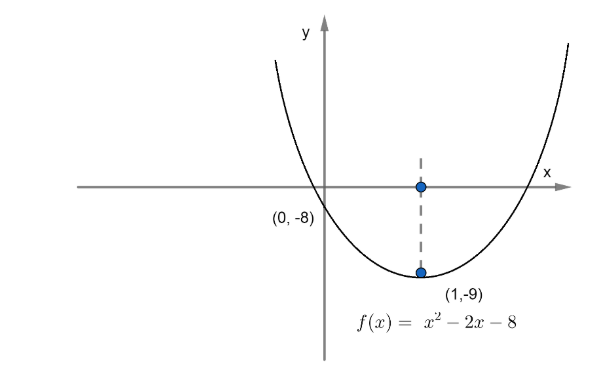
Note:It is important to note that we have used the fact that for equation $f\left( x \right)=a{{x}^{2}}+bx+c,a>0$the curve is concave upwards. Also, it is important to note that for critical points we have found x for which $\dfrac{d}{dx}\left( f\left( x \right) \right)=0$.