Question

How do you draw the graph of the given equation $5x+3y=-15$ using intercepts?

Answer 1

Hint: We start solving the problem by finding the intercept of the line with the x-axis using the fact that the value of the y coordinate is 0 on the x-axis. We then find the intercept of the line with the y-axis using the fact that the value of the x coordinate is 0 on the y-axis. We then represent both the obtained points on the graph and then join them together through a line to get the required plot.

Complete step-by-step solution:
According to the problem, we are asked to graph the equation $5x+3y=-15$ using intercepts.
We can see that the given equation $5x+3y=-15$ resembles the equation of line $ax+by+c=0$.
Let us find the intercept of the line with the x-axis. We know that the value of the y coordinate is 0 on the x-axis. Let us substitute $y=0$ in the line $5x+3y=-15$.
$\Rightarrow 5x+3\left( 0 \right)=-15$.
$\Rightarrow 5x=-15$.
$\Rightarrow x=\dfrac{-15}{5}$.
$\Rightarrow x=-3$.
So, the point on the line intersecting the x-axis is $A\left( -3,0 \right)$.
Now, let us find the intercept of the line with the y-axis. We know that the value of the x coordinate is 0 on the y-axis. Let us substitute $x=0$ in the line $5x+3y=-15$.
$\Rightarrow 5\left( 0 \right)+3y=-15$.
$\Rightarrow 3y=-15$.
$\Rightarrow y=\dfrac{-15}{3}$.
$\Rightarrow y=-5$.
So, the point on the line intersecting the y-axis is $B\left( 0,-5 \right)$.
Now, let us join points A and B to get the graph of the required equation as shown below.

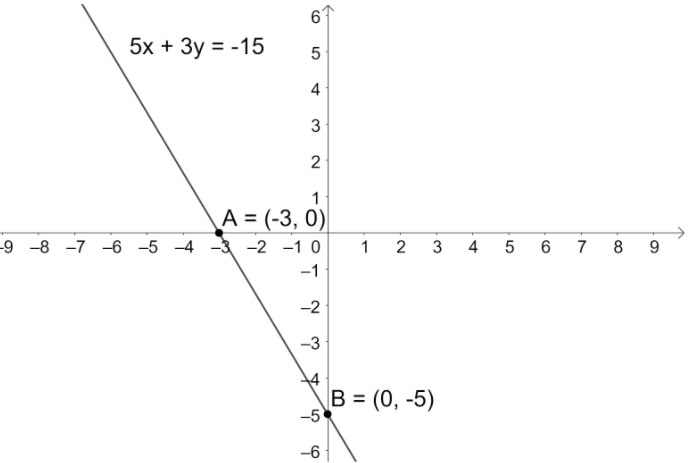
Note: Whenever we get this type of problem, we first try to find the figure that the given equation resembles in order to avoid mistakes. We can also solve this problem by making use of the fact that the intercept of the line is defined as $\dfrac{x}{a}+\dfrac{y}{b}=1$, where point of intersection on x-axis is $\left( a,0 \right)$ and on y-axis is $\left( 0,b \right)$. Similarly, we can expect problems to draw the plot of the equation $y={{x}^{2}}$.