
Draw the graph of the equation $y-2x=5$?
Answer
564.9k+ views
Hint: Plotting a graph depends on the type of the equation we have. A linear equation will always give a straight line, while a quadratic equation gives a parabolic shape. In the problem we have a linear equation, so we will get a straight line in the graph. For drawing a straight line, we need to have at least two points which satisfy the given linear equation. For finding the two points which satisfies the given line we need to take two points in the coordinate system like $\left( 0,a \right)$, $\left( b,0 \right)$. Now we will substitute the points in the given equation and calculate the values of $a$ and $b$. After getting these values we will plot these points in the coordinate system and join then to get the required result.
Complete step-by-step solution:
Given a linear equation $y-2x=5$.
Let us take a graph with the coordinate system is included, shown in below
Let us assume points $A\left( 0,a \right)$ and $B\left( b,0 \right)$ in the coordinate system and which will lie on the given linear equation. If the point $\left( {{x}_{1}},{{y}_{1}} \right)$ on the line $ax+by+x=0$, then $a{{x}_{1}}+b{{y}_{1}}+c=0$. Now the point $A\left( 0,a \right)$ lies on $y-2x=5$, then
$\begin{align}
& a-2\left( 0 \right)=5 \\
& \Rightarrow a=5 \\
\end{align}$
So, the point $A$ is $\left( 0,5 \right)$. Indicating the point $A$ in the above coordinate system, then
Now the point $B\left( b,0 \right)$ lies on $y-2x=5$, then
$\begin{align}
& 0-2\left( b \right)=5 \\
& \Rightarrow -2b=5 \\
& \Rightarrow b=-\dfrac{5}{2} \\
\end{align}$
So, the point $B$ is $\left( -\dfrac{5}{2},0 \right)$. Now plotting the point in the coordinate system, then
Now join both the points to get the plot of the given line.
Note: We can also draw a table which will give the values of $x$ and $y$ from the given relation. From the given relation we can have the value of $y$ as $y=5+2x$. Now will assume the values of $x$ from $-2$ to $2$ and calculates the values of $y$.
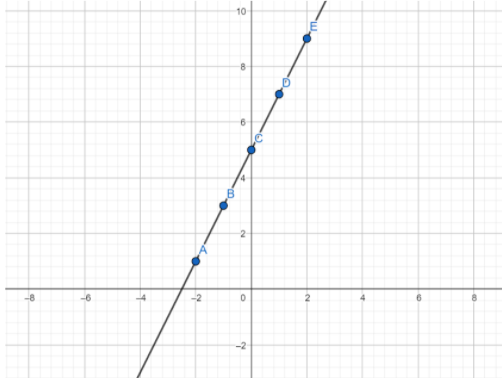
Now the points on the line are $\left( -2,1 \right),\left( -1,3 \right),\left( 0,5 \right),\left( 1,7 \right),\left( 2,9 \right)$. Plotting these points on the coordinate system, then
We can use any of the methods according to your convenience.
Complete step-by-step solution:
Given a linear equation $y-2x=5$.
Let us take a graph with the coordinate system is included, shown in below

Let us assume points $A\left( 0,a \right)$ and $B\left( b,0 \right)$ in the coordinate system and which will lie on the given linear equation. If the point $\left( {{x}_{1}},{{y}_{1}} \right)$ on the line $ax+by+x=0$, then $a{{x}_{1}}+b{{y}_{1}}+c=0$. Now the point $A\left( 0,a \right)$ lies on $y-2x=5$, then
$\begin{align}
& a-2\left( 0 \right)=5 \\
& \Rightarrow a=5 \\
\end{align}$
So, the point $A$ is $\left( 0,5 \right)$. Indicating the point $A$ in the above coordinate system, then

Now the point $B\left( b,0 \right)$ lies on $y-2x=5$, then
$\begin{align}
& 0-2\left( b \right)=5 \\
& \Rightarrow -2b=5 \\
& \Rightarrow b=-\dfrac{5}{2} \\
\end{align}$
So, the point $B$ is $\left( -\dfrac{5}{2},0 \right)$. Now plotting the point in the coordinate system, then

Now join both the points to get the plot of the given line.

Note: We can also draw a table which will give the values of $x$ and $y$ from the given relation. From the given relation we can have the value of $y$ as $y=5+2x$. Now will assume the values of $x$ from $-2$ to $2$ and calculates the values of $y$.
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=5+2x$ | $5+2\left( -2 \right)=1$ | $5+2\left( -1 \right)=3$ | $5+2\left( 0 \right)=5$ | $5+2\left( 1 \right)=7$ | $5+2\left( 2 \right)=9$ |
Now the points on the line are $\left( -2,1 \right),\left( -1,3 \right),\left( 0,5 \right),\left( 1,7 \right),\left( 2,9 \right)$. Plotting these points on the coordinate system, then

We can use any of the methods according to your convenience.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who gave "Inqilab Zindabad" slogan?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Who is the Brand Ambassador of Incredible India?




