
Draw the graph of the equation $ 2x + y = 6 $ . Shade the region bounded by the graph and the coordinate axis, also find the area.
Answer
577.8k+ views
Hint: To obtain a graph of a linear equation, we first assume some points of either variable(x or y) and then calculate the value of another variable using a given linear equation and then plot these points in x y plane on joining them we will get a graph of a linear equation. Then, find the coordinate of vertices of the triangle formed by a graph of a line and coordinate axis and hence it’s required area.
Complete step-by-step answer:
Given, linear equation is: $ 2x + y = 6 $
To plot a graph of a linear equation. We first assume some points of either of the variables and then calculate the value of another variable using the given linear equation.
Let $ x = 1, $ substituting it in a given linear equation. We have,
$
2(1) + y = 6 \\
\Rightarrow 2 + y = 6 \\
\Rightarrow y = 6 - 2 \\
\Rightarrow y = 4 \;
$
Therefore for $ x = 1, $ we have y = $ 4 $ .
Let $ x = 2, $ substituting it in a given linear equation. We have,
$
2(2) + y = 6 \\
\Rightarrow 4 + y = 6 \\
\Rightarrow y = 6 - 4 \\
\Rightarrow y = 2 \;
$
Therefore for $ x = 2, $ we have y = $ 2 $ .
Let $ x = 3, $ substituting it in a given linear equation. We have,
$
2(3) + y = 6 \\
\Rightarrow 6 + y = 6 \\
\Rightarrow y = 6 - 6 \\
\Rightarrow y = 0 \;
$
Therefore for $ x = 3, $ we have y = $ 0 $ .
Hence, from above we have a table:
Now, we will plot these points in the xy plane to find a graph of an equation $ 2x + y = 6 $ .
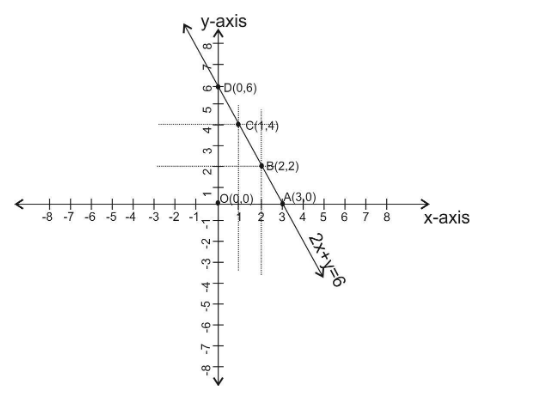
From the above graph we see that the graph of the linear equation meets the x-axis at $ (3,0) $ and y-axis at $ (0,6) $ .
Hence, coordinates of triangle OAB formed by graph of line and coordinate axis are given as:
$ O(0,0),\,\,A(3,0)\,\,and\,\,D(0,6) $ .
Therefore, area of triangle OAB = $ \dfrac{1}{2} \times OA \times OD $
$
\Rightarrow ar(\Delta OAD) = \dfrac{1}{2} \times 3 \times 6 \\
\Rightarrow ar(\Delta OAD) = 9 \;
$
Hence, the area of the triangle formed by a graph of a line and coordinate axis is $ 9\,\,square\,\,unit. $
Note: While plotting a graph of any equation. First calculate points very carefully. If all calculated points on plotting a graph do not come on a straight line then it is a hint of mistake. As for linear equations, graphs are always a straight line.
Complete step-by-step answer:
Given, linear equation is: $ 2x + y = 6 $
To plot a graph of a linear equation. We first assume some points of either of the variables and then calculate the value of another variable using the given linear equation.
Let $ x = 1, $ substituting it in a given linear equation. We have,
$
2(1) + y = 6 \\
\Rightarrow 2 + y = 6 \\
\Rightarrow y = 6 - 2 \\
\Rightarrow y = 4 \;
$
Therefore for $ x = 1, $ we have y = $ 4 $ .
Let $ x = 2, $ substituting it in a given linear equation. We have,
$
2(2) + y = 6 \\
\Rightarrow 4 + y = 6 \\
\Rightarrow y = 6 - 4 \\
\Rightarrow y = 2 \;
$
Therefore for $ x = 2, $ we have y = $ 2 $ .
Let $ x = 3, $ substituting it in a given linear equation. We have,
$
2(3) + y = 6 \\
\Rightarrow 6 + y = 6 \\
\Rightarrow y = 6 - 6 \\
\Rightarrow y = 0 \;
$
Therefore for $ x = 3, $ we have y = $ 0 $ .
Hence, from above we have a table:
| x | 1 | 2 | 3 |
| y | 4 | 2 | 0 |
Now, we will plot these points in the xy plane to find a graph of an equation $ 2x + y = 6 $ .

From the above graph we see that the graph of the linear equation meets the x-axis at $ (3,0) $ and y-axis at $ (0,6) $ .
Hence, coordinates of triangle OAB formed by graph of line and coordinate axis are given as:
$ O(0,0),\,\,A(3,0)\,\,and\,\,D(0,6) $ .
Therefore, area of triangle OAB = $ \dfrac{1}{2} \times OA \times OD $
$
\Rightarrow ar(\Delta OAD) = \dfrac{1}{2} \times 3 \times 6 \\
\Rightarrow ar(\Delta OAD) = 9 \;
$
Hence, the area of the triangle formed by a graph of a line and coordinate axis is $ 9\,\,square\,\,unit. $
Note: While plotting a graph of any equation. First calculate points very carefully. If all calculated points on plotting a graph do not come on a straight line then it is a hint of mistake. As for linear equations, graphs are always a straight line.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




