Question

Draw the graph of equation $2y+x=7$ and $2x+y=8$ on the same coordination system. Write the pt of intersection.

Answer 1

Hint: To solve this question, we first find two points through which the line passes by substitution. Then we plot the given line $2y+x=7.$ We follow a similar method to plot the second line $2x+y=8.$ Then we look for the point in the graph which is common to both the lines or an intersecting point as we call it.

Complete step by step solution:
The given question requires us to plot the lines $2y+x=7$ and $2x+y=8$ . In order to plot these, we need to find two points through which the given line passes through. Then we can draw the given line that passes through both the points. To find the points, we substitute the values of x and find the y-coordinate.
For the first line $2y+x=7,$ let us consider x=1. Substituting this in this equation,
$\Rightarrow 2y+1=7$
Subtracting 1 from both the sides,
$\Rightarrow 2y+1-1=7-1$
Dividing both sides by 2,
$\Rightarrow \dfrac{2}{2}y=\dfrac{6}{2}$
Simplifying this,
$\Rightarrow y=3$
Therefore, the first point is found out at $\left( 1,3 \right).$ Next, we substitute x=3.
Substituting this in the first equation itself,
$\Rightarrow 2y+3=7$
Subtracting 3 from both the sides,
$\Rightarrow 2y+3-3=7-3$
Dividing both sides by 2,
$\Rightarrow \dfrac{2}{2}y=\dfrac{4}{2}$
Simplifying this,
$\Rightarrow y=2$
Therefore, the second point is found out at $\left( 3,2 \right).$
Joining these two points by a line, we can graph the first line as shown in the figure below.

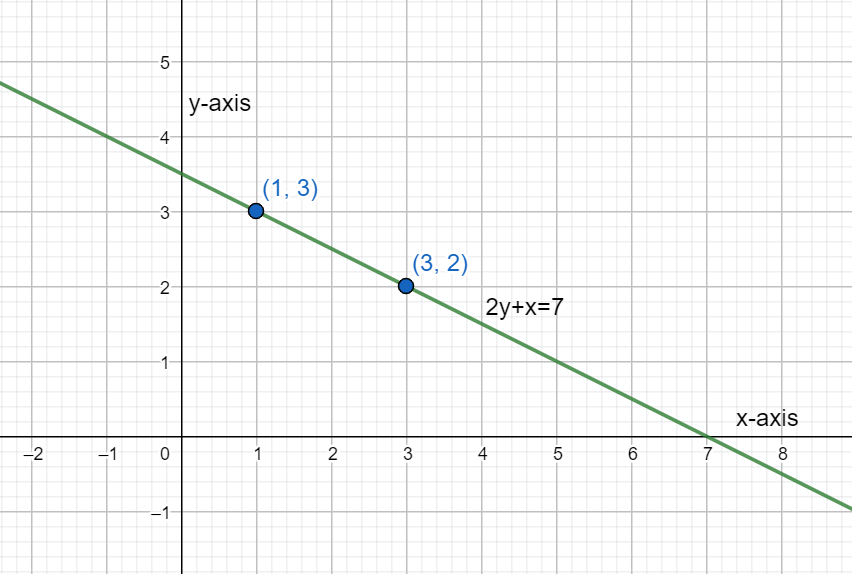
Next, we repeat the same steps for the second equation. For this second line $2x+y=8$ let us consider x=0. Substituting this in this equation,
$\Rightarrow 2\times 0+y=8$
Simplifying this, since 0 multiplied by 2 yields 0,
$\Rightarrow y=8$
Therefore, the first point is found out at $\left( 0,8 \right).$ Next, we substitute x=2.
Substituting this in the second equation itself,
$\Rightarrow 2\times 2+y=8$
Subtracting 4 from both the sides,
$\Rightarrow 4-4+y=8-4$
Simplifying 8 subtracted by 4 as 4,
$\Rightarrow y=4$
Therefore, the second point is found out at $\left( 2,4 \right).$
Joining these two points by a line, we can graph the first line as shown in the figure below.

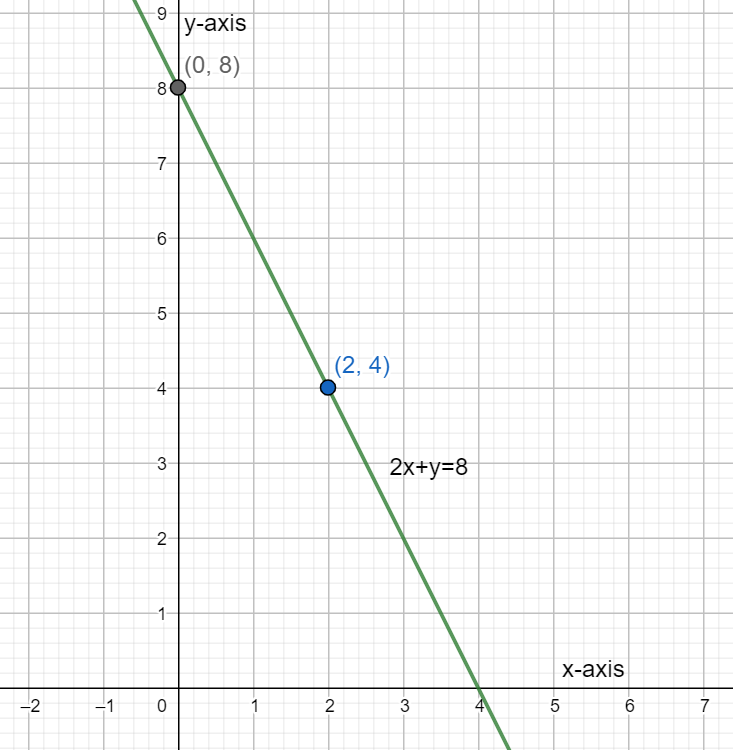
Now we plot both these lines on the same graph and check for a common or intersecting point.

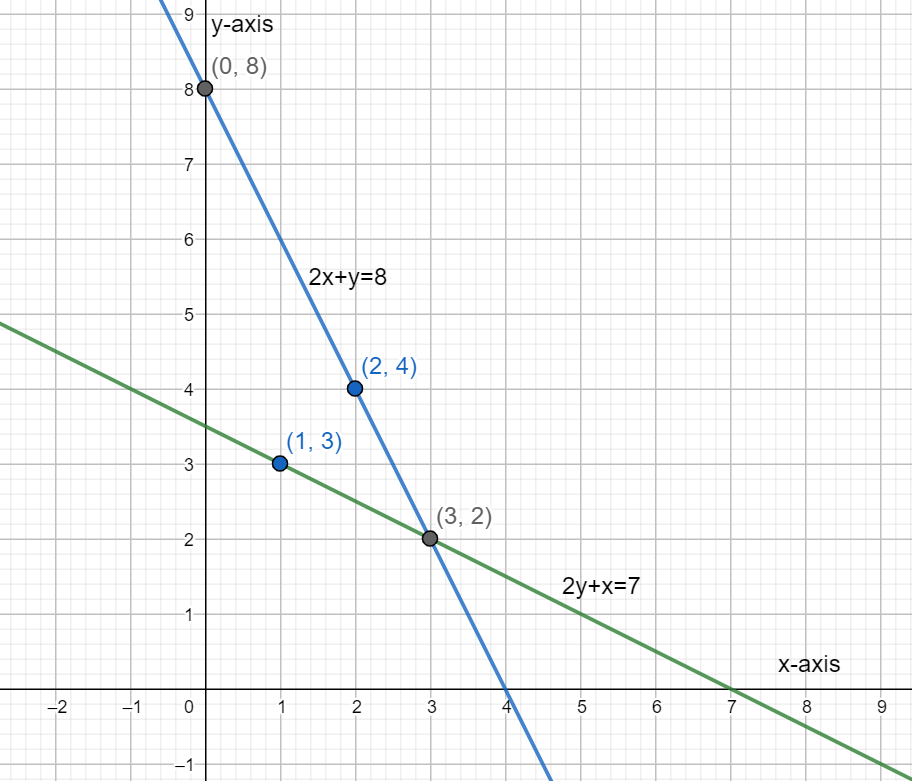
In this graph the green line represents the equation $2y+x=7$ whereas the blue line represents the equation $2x+y=8$ . We can see the two lines intersecting at a point $\left( 3,2 \right)$ which is the intersecting point for the given two lines.
Hence, we have drawn the graphs for the two line and found out the intersection point to be \[\left( 3,2 \right).\]


Note: Students need to have a good skill while graphing in order to plot these lines. We can also plot these by converting the equations to the slope intercept form which is given as $y=mx+c,$ where m is the slope and c is the y intercept. This method of slope intercept requires more time and students need to be patient while using this method.