Question

Draw the appropriate Venn diagram for each of the following:
(i)$${\left(A\cup B\right)}^{\prime }$$
(ii)$$A^{\prime }\cap B^{\prime }$$
(iii)$${\left(A\cap B\right)}^{\prime }$$
(iv)$$A^{\prime }\cup B^{\prime }$$

Answer 1

Hint: You can break the complex Venn diagrams into easier forms then use them to create the main Venn diagram it will help us understand the basics also.

Complete step-by-step answer:
Let’s start with the 1st part that is $${\left(A\cup B\right)}^{\prime }$$ .
So, for drawing Venn diagram of $${\left(A\cup B\right)}^{\prime }$$ , We have to break it down into parts this is what a normal Venn Diagram of $$\left(A\cup B\right)$$ looks like.

So. For drawing Venn diagram of $${\left(A\cup B\right)}^{\prime }$$ , We will invert the diagram of $$\left(A\cup B\right)$$ and then it looks like this.

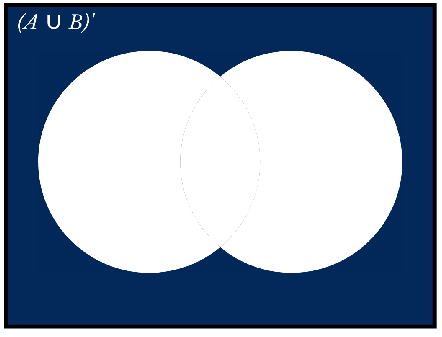
Here $$\left(A\cup B\right)$$ is represented by white color and $${\left(A\cup B\right)}^{\prime }$$ is represented by the navy blue color. Using simple Venn Diagrams to create complex diagrams is easy to grasp and easy for students to hold on to it.
Let’s go on to the 2nd part that is $$A^{\prime }\cap B^{\prime }$$ .
So, for drawing Venn diagrams of $$A^{\prime }\cap B^{\prime }$$ , We have to break it down into parts. This is what a normal Venn Diagram of $$A^{\prime }$$ and $$B^{\prime }$$ looks like.

Now, to get a Venn diagram of $$A^{\prime }\cap B^{\prime }$$ we will overlap Venn Diagrams of $$A^{\prime }$$ and $$B^{\prime }$$ , then we will easily get the Venn diagram.
After Overlapping Venn Diagrams of $$A^{\prime }$$ and $$B^{\prime }$$ , We Get this Venn Diagram. You must be thinking why it looks like the Venn diagram of $${\left(A\cup B\right)}^{\prime }$$. That’s because it is also the proof of one part of the De Morgan's laws that states $${\left(A\cup B\right)}^{\prime }=A^{\prime }\cap B^{\prime }$$ .

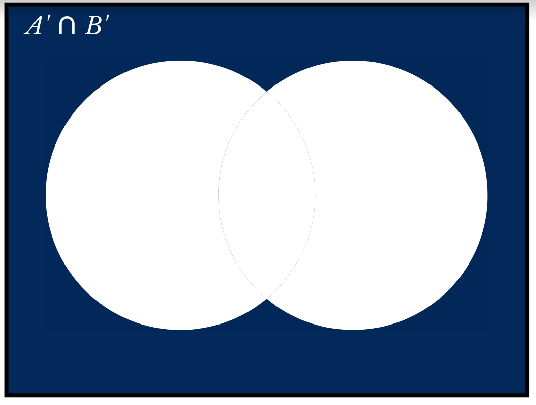
Let’s go on to the 3rd part now, that is $${\left(A\cap B\right)}^{\prime }$$ .
So, for drawing Venn diagram of $${\left(A\cap B\right)}^{\prime }$$ , We have to break it down into parts this is what a normal Venn Diagrams of $$\left(A\cap B\right)$$ looks like.

Now, To get the Venn diagram of $${\left(A\cap B\right)}^{\prime }$$ , We have to simply invert the Venn diagram of $$\left(A\cap B\right)$$ . After Inverting it looks like this.

Let’s go on to the 4th part now, that is $$A^{\prime }\cup B^{\prime }$$ .

So, for drawing a Venn diagram of $$A^{\prime }\cup B^{\prime }$$ , We have to break it down into parts. This is what a normal Venn Diagram of $$A^{\prime }$$ and $$B^{\prime }$$ looks like.

Now, to get the Venn diagram of $$A^{\prime }\cup B^{\prime }$$ , we will overlap the Venn Diagrams of $$A^{\prime }$$ and $$B^{\prime }$$. Then remove the unique part of $$A$$ and $$B$$ , As both of them appear in the complement of Opposite like we can see unique part of $$A$$ in $$B^{\prime }$$ and unique part of $$B$$ in $$A^{\prime }$$ .
After removing it we get this Venn diagram which only consists of $$\left(A\cap B\right)$$ . Here is the final Venn diagram of $$A^{\prime }\cup B^{\prime }$$ .

Additional Information: This can be done easily with the use of De Morgan's laws
Note: If we look closely at all four questions, we can easily state that these are the proofs of De Morgan's laws. Using these four we can easily prove both of De Morgarn’s laws.