Question

Draw rough sketches of the following. In $ \Delta \,PQR,\,PQ $ and $ PR $ are altitudes of the triangle.

Answer 1

Hint: Here, it is given that PQ and PR are two altitudes of triangle PQR. We see that in two altitude vertex P is common. Therefore, the angle between the two sides PQ and PR of the triangle is $ {90^0} $ . Hence, either of them is treated as altitude and other as base or vice versa.

Complete step-by-step answer:
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude.
Now we are supposed to draw $ \Delta \,PQR $ having PQ and PR as altitudes, therefore there should be a right angle in the triangle which is clear from definition of altitude.
 $ \therefore \,\Delta PQR $ , is a right angled triangle. Now we are to figure out which angle is the right angle.
[ $ \because $ Triangle can have only one $ {90^o} $ because by angle sum property of triangle sum of three angles of triangle is $ {180^o} $ .If a triangle has two $ {90^o} $ it will contradict the angle sum property of the triangle.]
We know that altitudes PQ and PR have the same vertex $ P,\,\therefore \,\Delta PQR $ must be right angled at P.

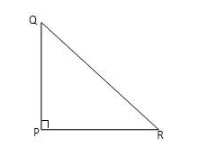
Now at last to draw a rough sketch we have $ \angle P = {90^o},\,PQ $ and PR are altitudes. Third side QR left should be hypotenuse.So from above information we can draw rough sketch

Note: To draw altitudes always keep in mind the definition of altitudes that is, an altitude is a line drawn from a triangle's vertex down to the opposite base, so that the constructed line is perpendicular to the base and hence in right angle there are two lines which are perpendicular to each other.