Question

Draw graphs showing the variation of acceleration due to gravity with $\left( a \right)$ height above the earth's surface, ($b$) depth below the earth's surface.

Answer 1

Hint: Acceleration due to gravity is the acceleration gained by an object due to gravitational force. Its SI unit is \[m/{{s}^{2}}\].It has both magnitude and direction, hence, it's a vector quantity. The acceleration due to gravity decreases linearly with depth and in the middle of the earth, it becomes zero which can seem to you counter-intuitive.
Formula used:
$F=\dfrac{GMm}{{{\left( R+h \right)}^{2}}}$

Complete answer:
$\left( a \right)$Height above the earth's surface:
Take a test mass ($m$) at a height ($h$) from the surface of the earth. Now, the force working on the test mass due to gravity is;
\[F\text{ }=\text{ }\dfrac{GMm}{{{\left( R+h \right)}^{2}}}\]
Where $M$ is that the mass of earth and $R$ is that the radius of the earth. The acceleration due to gravity at a particular height is ‘h’ then,
\[m{{g}_{h}}=\text{ }\dfrac{GMm}{{{\left( R+h \right)}^{2}}}\]
\[\Rightarrow {{g}_{h}}=\text{ }\dfrac{GM}{\left[ {{R}^{2}}{{\left( 1+\text{ }h/R \right)}^{2}}\text{ } \right]}\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }\left( 2 \right)\]
The acceleration due to gravity on the surface of the earth is given by;
\[g\text{ }=\text{ }\dfrac{GM}{{{R}^{2}}}\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }\left( 3 \right)\]
On dividing equation ($3$) and ($2$) we get,
${g_h}{\text{ }} = {\text{ }}g{\text{ }}{\left( {1 + \dfrac{h}{R}} \right)^{ - 2}}.{\text{ }}.{\text{
}}.{\text{ }}.{\text{ }}.{\text{ }}.{\text{ }}\left( 4 \right)$

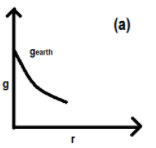
This is the acceleration due to gravity at a height above the surface of the earth. Observing the above formula carefully we will say that the worth of g decreases with the increase tall of an object and therefore the value of g becomes zero at infinite distance from the earth.
$\left( b \right)$Depth below the earth's surface:
Consider a test mass ($m$) taken to a distance ($d$) below the earth’s surface, the acceleration due to gravity that time (${{g}_{d}}$) is obtained by taking the worth of $g$ in terms of density.
On the surface of the earth, the worth of g is given by;
\[g\text{ }=\text{ }4/3\text{ }\times \text{ }\pi \rho RG\]
At a distance ($d$) below the earth’s surface, the acceleration due to gravity is given by;
\[{{g}_{d}}\text{ }=\text{ }4/3\text{ }\times \text{ }\pi \rho \text{ }\times \text{ }\left( R\text{ }\text{ }d \right)\text{ }G\]
On dividing the above equations, we get,
\[{{g}_{d}}\text{ }=\text{ }g\text{ }\dfrac{\left( R\text{ }\text{ }d \right)}{R}\]
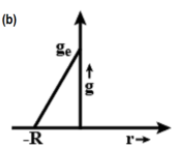
When the depth\[d\text{ }=\text{ }0\], the worth of g on the surface of the earth \[{{g}_{d}}\text{ }=\text{ }g.\]
When the depth\[d\text{ }=\text{ }R\], the worth of g at the centre of the earth ${{g}_{d}}=0$

Additional Information:
It depends on the mass and radius of the earth. All bodies experience an equivalent acceleration due to gravity, regardless of its mass. Its value on earth depends upon the mass of the world and not the mass of the thing.

Note:
For an object placed at a height h, the acceleration due to gravity is a smaller amount as compared thereto placed on the surface. As depth increases, the value of acceleration due to gravity ($g$) falls. The value of $g$ is more at the equator and fewer at poles.