Question

Draw $\angle POQ$ of measure ${75^ \circ }$ and find its line of symmetry.

Answer 1

Hint: We will draw a ray $OP$ and with $O$ as centre, draw an angle of ${90^ \circ }$. Then, draw an angle of ${75^ \circ }$ using appropriate steps of construction. Then, draw the line of symmetry by drawing the angle bisector of the $\angle POQ$.

Complete step-by-step answer:
First draw a ray and name it $OP$.

Now, take $O$ as centre and take a suitable radius, and draw an arc cutting $OP$ at $T$.
Now, keep $T$ as centre and draw arcs cutting the previous arc at point $S$ with the same radius.
Similarly, draw two arcs \[R\] and \[M\]with $S$ as centre and then draw an arc which intersects the previous arc at $M$ from point $R$.
Join the line $MO$ using a dotted line draw an angle of ${90^ \circ }$

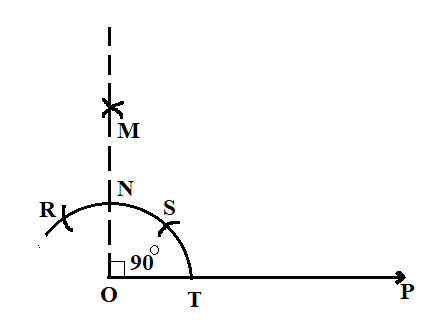
We will now draw two arcs cutting each other at $Q$ from the points $S$ and $N$.
Join the line $PO$ and thus the measure of angle $\angle POQ$ is ${75^ \circ }$.

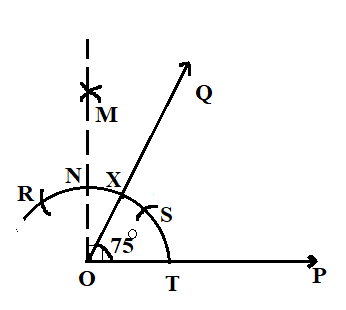
We also have to make its line of symmetry.
We will draw two arcs from $X$ and $T$ with a fixed radius, intersecting at point Y.
Join the line $OY$ which is the line of symmetry of the angle $\angle POQ$.

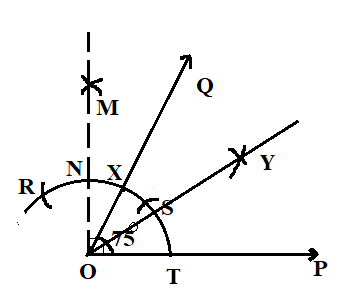
Note: The line of symmetry is the line that divides the line segment in two equal parts. Also, while constructing the angle, do not change the radius, keep the compass fixed at the centre and use a sharp pencil to get points neatly.