Question

How do you draw and angle $ ABC $ , with $ A = 35^\circ ,AC = 6cm $ and $ C = 65^\circ $ ?

Answer 1

Hint: In this question, we simply need to use a protractor to draw a $ 6cm $ line segment and then construct $ 35^\circ $ and $ 65^\circ $ angles respectively. On constructing these angles, the intersection of these lines will give us the required angle.

Complete step by step solution:
Given data,
 $
  AC = 6cm \\
  \angle A = 35^\circ \\
  \angle C = 65^\circ \\
  \angle ABC = ? \;
  $
Step 1: Construct a line segment of length $ 6cm $ .
First of all, we are given the length of the line segment $ AC $ .
So, let’s construct a line segment $ AC $ of magnitude $ 6cm $ .
Position the midpoint of the protractor at point $ A $ and construct $ 6cm $ long line segment.

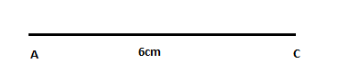
Step 2: Construct an angle $ A = 35^\circ $ .
Now, we have to construct an angle $ A = 35^\circ $ .
For that, place the midpoint of the protractor at point $ A $ and mark a point at $ 35^\circ $ and then join that point with vertex $ A $ .

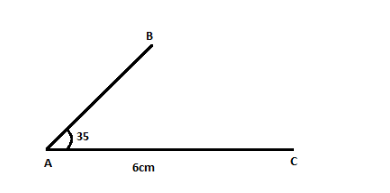
Hence, we have constructed angle $ A = 35^\circ $ .

Step 3: Construct an angle $ C = 65^\circ $ .
Now, we have to construct an angle $ C = 65^\circ $ .
So, similarly place the midpoint of protractor at point $ C $ and mark a point at
 $ 65^\circ $ and then join that point with vertex $ C $ .

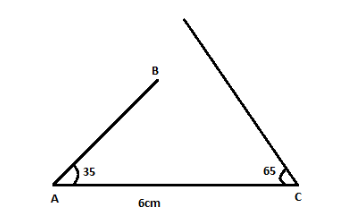
Hence, we have constructed angle $ C = 65^\circ $ .
The intersection point of these two lines drawn above will give us the value of $ \angle ABC $ .

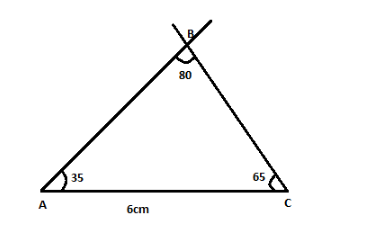
Therefore, our required angle $ ABC = 80^\circ $ .

Note: We can cross-check our answer by using angle sum property of a triangle.
 $
   \Rightarrow \angle A + \angle B + \angle C = 180^\circ \\
   \Rightarrow 35^\circ + \angle B + 65^\circ = 180^\circ \\
   \Rightarrow \angle B = 180^\circ - 35^\circ - 65^\circ \\
   \Rightarrow \angle B = 80^\circ \;
  $
Hence, our answer $ \angle ABC = 80^\circ $ is correct.