Question

Draw an isosceles triangle ABC in which AB=AC=6 cm and BC=5 cm. Construct a triangle PQR similar to triangle ABC in which PQ=8 cm. Also justify the construction.

Answer 1

Hint: The ratio of the corresponding sides of the similar triangles is always equal. So find the ratio of the side of the triangle ABC with its corresponding side of triangle PQR. The remaining corresponding sides will also have the same ratio. Using this ratio we can find the unknown values of sides with the help of known values.

Complete step-by-step answer:
We are given that triangle ABC is an isosceles triangle and AB=AC=6cm, BC=5cm.
It is also given in the question that triangles PQR and ABC are similar which means triangle PQR is also an isosceles triangle.
      

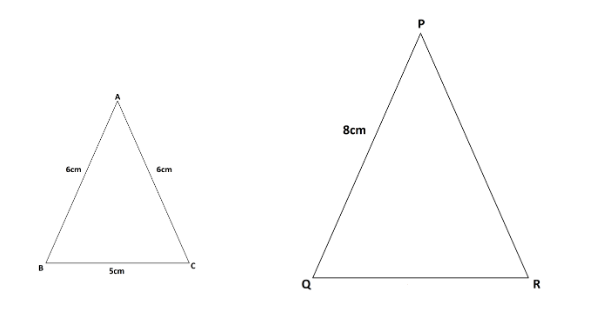
From the above diagrams, we can say that side AB is corresponding to side PQ, side BC is corresponding to side QR, side AC is corresponding to side PR.
This means $ \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AC}}{{PR}} $ and PQR is an isosceles triangle so PQ=PR.
We are already given with the values of AB, BC, AC and QR. We need to find the values of PQ, PR to construct the triangle PQR.
AB=6cm, BC=5cm, AC=6cm, PQ=PR=8cm, QR=?
 $
  \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AC}}{{PR}} \\
  \dfrac{6}{8} = \dfrac{5}{{QR}} = \dfrac{6}{8} \\
  \dfrac{6}{8} = \dfrac{5}{{QR}} \\
  QR = \dfrac{{5 \times 8}}{6} \\
  QR = \dfrac{{40}}{6} \\
  QR = \dfrac{{20}}{3}cm \\
  $
Therefore, side $ QR = \dfrac{{20}}{3}cm $ of the triangle PQR.
Justification:
As these both are similar triangles the ratio of the corresponding sides of the similar triangles is always equal. So let us see if they are equal or not.
 $ \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AC}}{{PR}} $
AB=AC=6cm, BC=5cm, PQ=PR=8cm, QR=20/3cm
 $
   \to \dfrac{6}{8} = \dfrac{5}{{\left( {\dfrac{{20}}{3}} \right)}} = \dfrac{6}{8} \\
   \to \dfrac{3}{4} = \dfrac{{5 \times 3}}{{20}} = \dfrac{3}{4} \\
   \to \dfrac{3}{4} = \dfrac{{15}}{{20}} = \dfrac{3}{4} \\
   \to \dfrac{3}{4} = \dfrac{3}{4} = \dfrac{3}{4} \\
  $
Therefore justified.

Note: The corresponding angles are also equal in similar triangles. Some of the similar triangles can have different corresponding values and some of the sides can be turned or flipped.