Question

Draw an angle of measure\[{147^ \circ }\]and construct its bisector.

Answer 1

Hint: Geometry is the branch of mathematics which studies about the size, shapes, position angles and dimension. To draw any angle bisector we need a compass to mark an arc for that angle to draw.

Complete step-by-step answer:
Given to draw an angle of measure\[{147^ \circ }\]
The angle which is to be drawn is in between the two lines hence, we have to draw a straight line QR which will be the base for the angle.
Since it is not possible to draw an angle of measure \[{147^ \circ }\]using the compass hence use the protractor to draw an angle \[{147^ \circ }\]of by placing the protractor on the base line QR at Q and mark the point naming it P at an angle\[{147^ \circ }\]and join the line PQ.
Hence we get the angle \[\angle PQR = {147^ \circ }\]
Now we need to find the bisector of \[\angle PQR = {147^ \circ }\]
By using compass join point S which is on the line PQ with the point T on the line QR
Now S and T as the centers and with the radius more than\[\dfrac{1}{2}ST\], draw an arc to intersect each other and let them intersect at the point O
Now join the line OQ

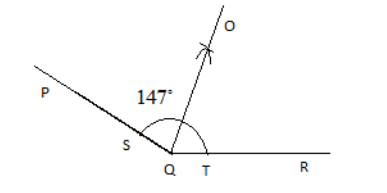
Therefore OQ is the bisector of\[\angle PQR = {147^ \circ }\], where
\[\angle PQO = \angle RQO = \dfrac{{147}}{2} = {73.5^ \circ }\]

Note: It is to be noted down here that the angle bisector is the priority thing which is to be kept in mind while plotting the angle. Always the angle could be plotted by using the concept of angle bisectors.