Question

How do you draw an angle of \[{710^ \circ }\] in standard position?

Answer 1

Hint: We all know that the last maximum angle on the rounder is \[{360^ \circ }\] . But here we are asked to find the angle almost double the maximum angle. So we can draw this big angle also with the help of standard conditions. This angle is just \[{10^ \circ }\] less than twice the maximum angle on the rounder.so this is the main point. Let’s start.

Complete step by step solution:
Now we know that, this angle is \[{10^ \circ }\] less than double the \[{360^ \circ }\]
That is \[{710^ \circ } = {360^ \circ } \times 2 - {10^ \circ }\]
This clearly says that one full angle should be taken. So keeping the point on centre and starting as anticlockwise draw the first half part;

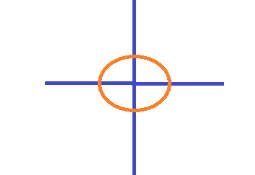
This is complete one full angle.
Now moving forward, we will take the remaining angle. Now we will take that \[{10^ \circ }\] as the reference angle and we know that it will fall in fourth quadrant so,

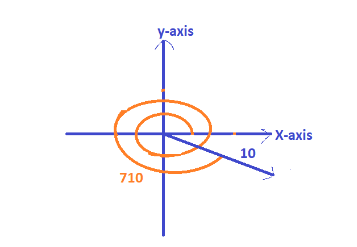
This is the perfectly drawn angle of the measures we are given.

Note: Note that standard position is not just drawing the angle it totally means the vertex is at centre and the initial side should be on the positive X axis. Also note that the reference angles are different for all four quadrants. Like it is the acute angle made by its terminal side and the horizontal axis.