Question

How do you draw an angle 440 degree in standard position?

Answer 1

Hint: We will use the circular function property to solve the above question. Since, we know that total angle inscribed inside a circle is $360{}^\circ $ and since $440{}^\circ $ is greater than $360{}^\circ $ so, we have to move one circular rotation plus the left angle $\left( 440{}^\circ -360{}^\circ \right)=80{}^\circ $ to represent $440{}^\circ $. Thus, we can also say that $440{}^\circ $ is equivalent to $80{}^\circ $. So, we will draw the angle of $80{}^\circ $.

Complete answer:
We will use the concept of circular function to solve the above question. Circular functions are those functions which repeat their value after a period of $2\pi $. Sine and Cosine are two fundamental circular functions whose value gets repeated after a certain period of $2\pi $.
The total angle or complete angle made by a circle is $2\pi $i.e. $360{}^\circ $.
Since, we have to draw an angle of 440 degree in standard position, and we can see that $440{}^\circ $is greater than $360{}^\circ $ so at first we will move a one circular rotation in anticlockwise direction and then we will represent the remaining angle i.e. $\left( 440{}^\circ -360{}^\circ \right)=80{}^\circ $by moving another rotation in anticlockwise direction.
So, we will draw an angle of $80{}^\circ $ which is equivalent to $440{}^\circ $ with the help of a protector.
At first, we will draw a line segment AB and then we will put the centre of the protector at one vertex and then we will mark an angle of $80{}^\circ $ and then join the vertex with the marked point with a line.
The line which we have obtained is so will represent the angle of 440 degree in standard position.
 

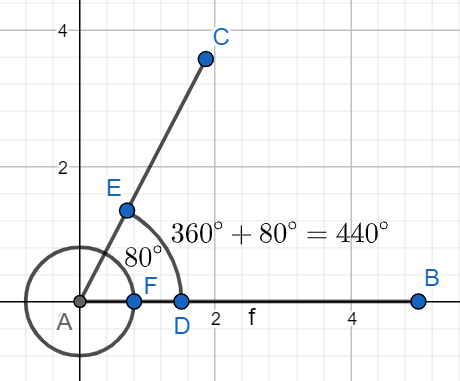
This is our required solution.

Note: Students are required to note that when we have to represent a positive angle we usually move in anticlockwise direction and when we have to represent a negative angle we move in clockwise direction.