Question

Draw a triangle ABC with side BC = 7 cm, $ \angle B=45{}^\circ ,\angle A=105{}^\circ $ . Then, construct a triangle whose sides are $ \dfrac{3}{4} $ ​ times the corresponding sides of triangle ABC.

Answer 1

Hint: Construct the triangle ABC using the basic methods. To draw the triangle EBD, draw a ray BX at an acute angle to line BC on the opposite side of A and mark 4 equidistant points B1​, B2​, B3​, B4​ on ray BX. Join B3​ and C. Draw B4​D parallel to B3​C and ED parallel to AC. Hence, the triangle EBD is the required triangle.

Complete step-by-step answer:
In this question, we need to construct a triangle ABC with side BC = 7 cm, $ \angle B=45{}^\circ ,\angle A=105{}^\circ $ . Then, we need to construct a triangle whose sides are $ \dfrac{4}{3} $ ​ times the corresponding sides of triangle ABC.
First, we will find the measure of $ \angle C $ using the angle sum property of a triangle on triangle ABC.
 $ \angle A+\angle B+\angle C=180{}^\circ $
 $ 105{}^\circ +45{}^\circ +\angle C=180{}^\circ $
 $ \angle C=180{}^\circ -150{}^\circ $
 $ \angle C=30{}^\circ $
Now, we will start with the construction.
The steps for the construction are given below.
Constructing triangle ABC:
Step 1: Draw base BC of length 7 cm.
Step 2: Draw a ray at an angle of $ 45{}^\circ $ with line BC from point B.
Step 3: Draw a ray at an angle $ 30{}^\circ $ from line CB from point C and mark the intersection point of the rays from B and C as A.
Step 4: Join AB and AC.
Triangle ABC is the required triangle.
 

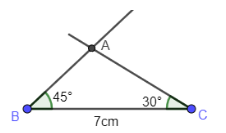
Triangle ABC is the required triangle.

For constructing triangle EBD whose sides are ​ times the corresponding sides of triangle ABC.
Step 1: Draw a ray BX at an acute angle to line BC on the opposite side of A.

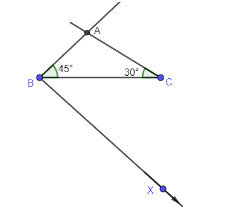
Step 2: Mark 4 equidistant points B1​, B2​, B3​, B4​ on ray BX.
Step 3: Join B3​ and C.
Step 4: Draw B4​D parallel to B3​C and label the intersection on the extension of BC as D.

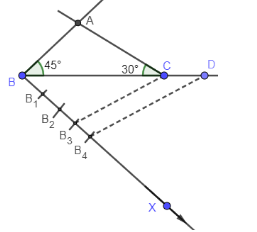
Step 5: Draw DE parallel to CA and label the intersection with the extension of BA as E

Triangle EBD is the required triangle.
The following figure shows the final construction:

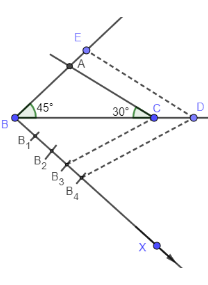
Note: In this question, it is very important to know about the angle sum property of a triangle.The angle sum property of a triangle states that the angles of a triangle always add up to $ 180{}^\circ $ . Every triangle has three angles and whether it is an acute, obtuse, or right triangle, the angles sum to $ 180{}^\circ $ . For example, in triangle ABC, angle A + angle B + angle C = $ 180{}^\circ $ .