Question

Draw a transverse common tangent of length 8 cm to two circles of radii 4 cm and 2 cm.

Answer 1

Hint: Here, we will proceed by using scale and compass in order to draw line segment AB and two circles of radii 4 cm and 2 cm with centres at A and B respectively. Then, we will draw a concentric circle of radius 6 cm to the circle of 4 cm radius.

Complete step-by-step answer:
Here, the length of the common tangent between two circles having radii 4 cm and 2 cm should be 8 cm.
The following steps of construction in order to draw the required transverse common tangent are given below:
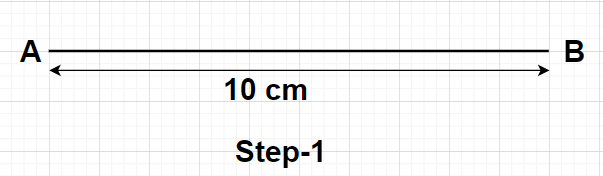
Step1- Firstly, we will draw a line segment of length 10 cm using a scale and name the two ends of this line segment as A and B. So, AB is a line segment of length 10 cm which is actually the distance between the centres of the two circles.

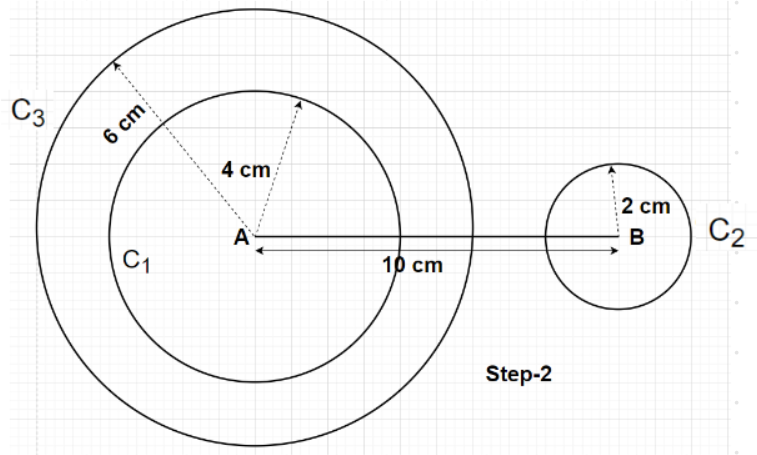
Step2- Using the compass, draw a circle ${{\text{C}}_1}$ with the centre of that circle at point A and having a radius as 4 cm. Now, draw another circle ${{\text{C}}_2}$ with the centre of that circle at point B and having a radius of 2 cm. Now, draw another circle ${{\text{C}}_3}$ with centre of that circle at point A and having radius equal to the sum of the radii of circles ${{\text{C}}_1}$ and ${{\text{C}}_2}$ i.e., 4+2=6 cm. So, the circle ${{\text{C}}_3}$ is having a radius of 6 cm. This circle ${{\text{C}}_3}$ is concentric with the circle ${{\text{C}}_1}$.

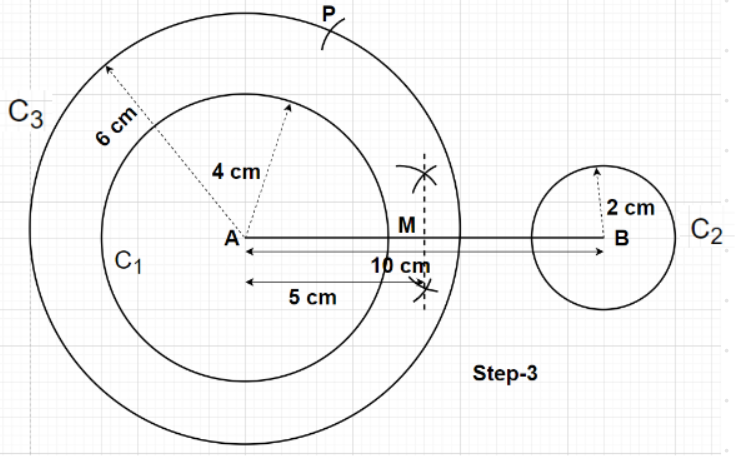
Step3- Now, with the help of the compass bisect the line segment AB to get the midpoint M of this line segment. With M as the centre and AM or BM as the radius where AM=BM=5 cm, draw an arc to cut the circle ${{\text{C}}_3}$ at point P which lies on the circumference of the circle ${{\text{C}}_3}$ as shown in figure.

Step4- Now, join the points A and P together in order to form a line AP which cuts the circle ${{\text{C}}_1}$ at point Q which lies at the circumference of the circle ${{\text{C}}_1}$. Draw a line from point B, parallel to the line segment AQP. Name the point as R where this drawn parallel line cuts the circle ${{\text{C}}_2}$. Now join the points Q and R by a straight line using the scale. This line segment QR is the required transverse common tangent of length 8 cm to two circles of radii 4 cm and 2 cm which can be verified by measuring its length which will eventually be equal to 8 cm.

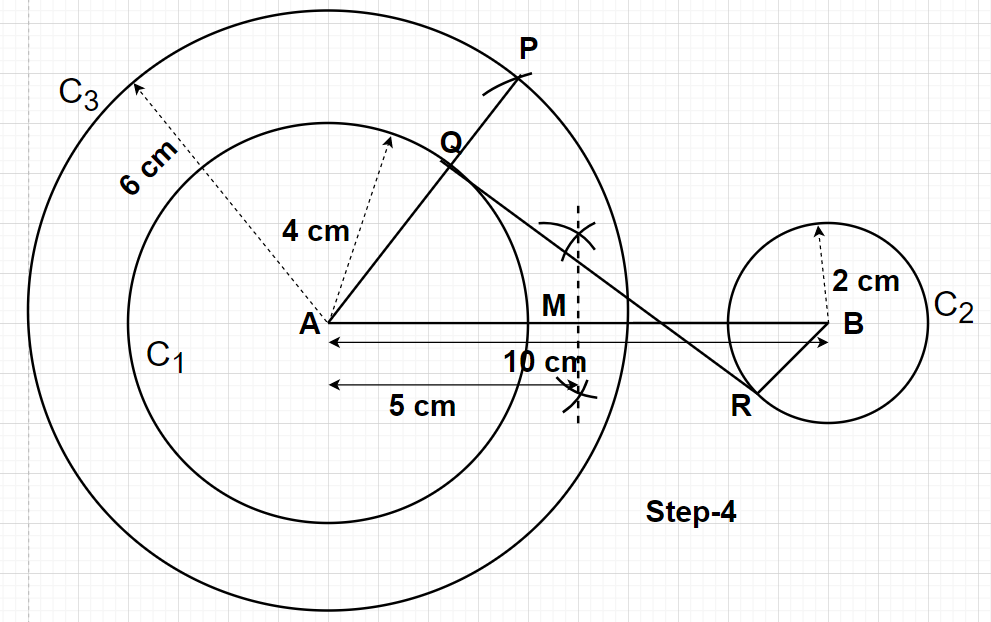
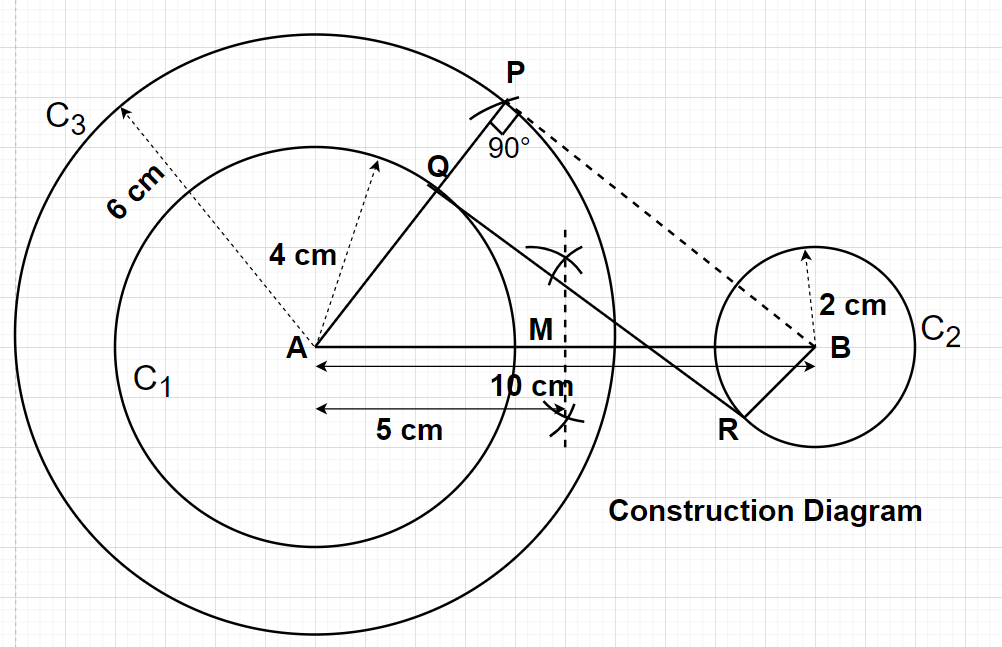
Since, the angle made by the tangent with the radius line is always equal to ${90^0}$. So, from the figure we can write $\angle {\text{AQR}} = {90^0}$. Here, we will join the points P and B by a dotted line with the help of the scale. Clearly, the lines QR and PB are parallel to each other.
So, $\angle {\text{APB}} = \angle {\text{AQR}} = {90^0}$
As according to Pythagoras Theorem in any right angled triangle, ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$
In right angled triangle APB, we can write
$
  {\left( {{\text{AB}}} \right)^2} = {\left( {{\text{PB}}} \right)^2} + {\left( {{\text{AP}}} \right)^2} \\
   \Rightarrow {\text{AB}} = \sqrt {{{\left( {{\text{PB}}} \right)}^2} + {{\left( {{\text{AP}}} \right)}^2}} \\
 $
As, PB=QR=8 cm and AP is the radius of circle ${{\text{C}}_3}$ i.e., AP=6 cm
$
   \Rightarrow {\text{AB}} = \sqrt {{{\left( {\text{8}} \right)}^2} + {{\left( {\text{6}} \right)}^2}} \\
   \Rightarrow {\text{AB}} = \sqrt {64 + 36} \\
   \Rightarrow {\text{AB}} = \sqrt {100} \\
   \Rightarrow {\text{AB}} = 10{\text{ cm}} \\
 $
So, the distance between the centres of these two circles is 10 cm.

Note: In this particular problem, for bisection of line segment AB we will place the fixed end of the compass at point A and make two arcs with radius more than half of the length of line segment AB and then, similarly we will place the fixed end at point B and make two more arcs with the same radius. Now, we will join the points where the two pairs of arcs will intersect by a dotted line and the point where this dotted line intersects the line AB is the midpoint of AB named as point M.