Question

Draw a tangent to a circle.

Answer 1

Hint:
Here we need to draw a tangent to a circle. To draw that, we will first draw a circle using the compass and then we will join the point of center of circle to any point on the circle, which will give us the radius of the circle and then we will draw a perpendicular line at the end point of the radius using the compass. This perpendicular line will be the required tangent to the circle.

Complete step by step solution:
 We need to draw a tangent to a circle.
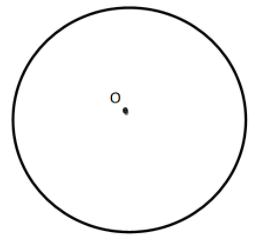
We will first draw a circle of any radius using the compass and we will name the center point of the circle as point $O$.

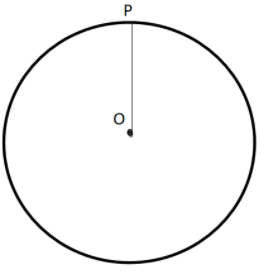
Now, we will join the point of the center of the circle to any point $P$ on the circle.

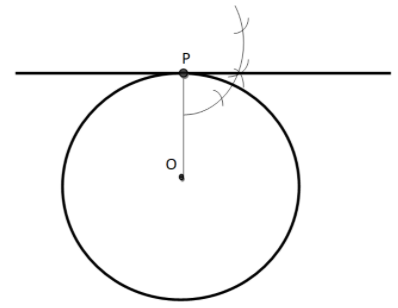
Now, we will draw the perpendicular at the point $P$ using the compass.

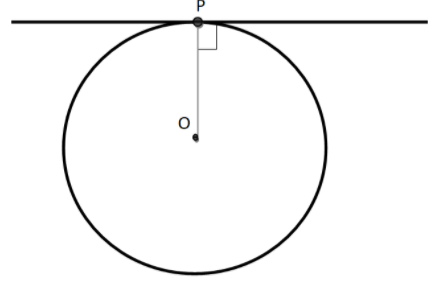
We will redraw the above figure of the circle with tangent.

Note:
Tangent is defined as a line that touches the circle at only one point. Remember that the tangent never intersects the circle or never crosses the circle. A tangent always forms an angle of ${{90}^{\circ }}$ with the radius of the circle at the point of tangency. The length of two tangents drawn from the same external point to the circle is equal. Two tangents drawn on the circle are parallel if both the tangents are drawn at the end points of the diameter of the circle and in other words we can say that the tangents drawn at the end points of the diameter are parallel.