Question

Draw a square of area 25 square cm and find its perimeter.

Answer 1

Hint – In this particular question use the concept that the area of the square is the square of its side length so first calculate the side of the square, later on use the concept of perimeter so use these properties to reach the solution of the question.

Complete step-by-step answer:

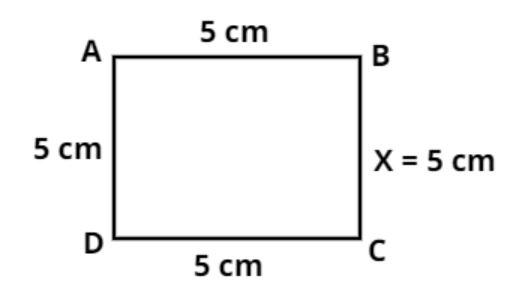
Given data:
Square has an area of 25 square cm.
Consider the square ABCD as shown in the above figure.
As we all know that the area of the square is the square of its side length, if the side length is in meter then its unit is square meter, if the side length is in centimeter then its unit is square centimeter.
Let the side of the square be X cm.
Let the area of the square be denoted by A.
So A = $X^2$Cm2...................... (1)
Now it is given that A = 25 square cm.
So substitute this value in equation (1) we have,
$\Rightarrow X^2=25$
Now take square root on the both sides we have,
$\Rightarrow \sqrt{X^2}=\sqrt{25}$
$\Rightarrow X=\pm 5$
Negative side is not possible, so the side of the square is 5 cm.
As shown in the figure.
Now as we know that in the square all the sides are equal as shown in the figure.
So the length of all the sides of the square = 5 cm.
Now as we know that the perimeter of any shape is the sum of all the sides.
So the perimeter of the square is the sum of all the sides of the square.
Let the perimeter be denoted by P.
So, P = 5 + 5 + 5 + 5 = 20 cm.
So this is the required perimeter of the square.

Note – Whenever we face such types of questions the key concept we have to remember is that the perimeter of any shape is the sum of all the side lengths of the shape, so first calculate the side of the square as above then add all the sides of the square and simplify which is the required perimeter of the square.