Question

Draw a sketch of a pair of similar triangles. Label them. Show their corresponding angles by the same signs. Show the lengths of corresponding sides by numbers in proportion.

Answer 1

Hint: If we measure by taking the sum of the angles of a triangle, then it would be \[180^\circ \]. Similar triangles are those that are the same in structure or shape but different in sizes (lengths). They will be having the same corresponding angles so while drawing the triangles these points are the key elements.

Complete step-by-step answer:

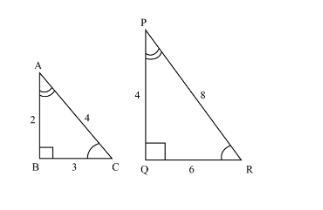
It is asked to draw a sketch of a pair of similar triangles, as we know that the similar triangle looks the same in structure and has the same corresponding angles but has different size .
So the pair of similar triangles will be as follows. From the drawn triangles it can be said that \[\angle B = \angle Q = 90^\circ \], \[\angle C = \angle R\] and \[\angle A = \angle P\] so all the angles are equal.
Speaking about the sides, the side AB and PQ are in the ratio of \[2:4 = 1:2\], the side BC and QR are \[3:6 = 1:2\] and the sides CA and RP are in the ratio of \[4:8 = 1:2\].
All the three sides are in the ratio of \[1:2\], it means that the two triangles will be the same in shape or structure but different in size.
Therefore, the pair of similar triangles is sketched according to the statements.

Note: In the solution, we took one of the sides as \[90^\circ \], we can even draw the pair of similar triangles using any angles but we should keep in mind that the corresponding angles should be equal because the angle will be the response for the shape of the triangle. We should keep in mind that while assuming the angles, the sum of the all angles should not exceed \[180^\circ \].