Question

Draw a right triangle \[PQR\], right angled at Q such that \[PQ = 3cm\], \[QR = 4cm\]. Now construct \[\vartriangle AQB\] similar to $\vartriangle PQR$ each of whose sides is $\dfrac{7}{5}$ times the corresponding sides of $\vartriangle PQR$

Answer 1

Hint: Using scale factor for the given triangle draw the next triangle.Then we're given a triangle, so via a means of scale issue homes we can draw the subsequent required triangle via a means of extending the ray, then dividing the ray on the unit period after which draws parallel traces at the size values after which entire the triangle.

Complete step by step solution:
Given a $\vartriangle PQR$ in which $\angle Q = {90^o}$, $PQ = 4cm$ and $QR = 3cm$
STEPS OF CONSTRUCTION
Draw a line segment $PQ = 4cm$
At Q make $\angle PQY = {90^o}$
Take Q as the centre and radius 3cm draw an Arc cutting QY at R.
Join PR to obtain the$\vartriangle PQR$
Through Q as centre and radius 3cm draw an Arc cutting QY at R.
Join PR to obtain the $\vartriangle PQR$
Through Q, construct an acute angle $\angle PQR( < {90^o})$opposite to the vertex.
Mark 5 points ${Q_1},{Q_2},{Q_3},{Q_4},{Q_5}$ in $QX$ such that$Q{Q_1} = {Q_1}{Q_2} = {Q_2}{Q_3} = {Q_3}{Q_4} = {Q_4}{Q_5}$
Join${Q_5}P$
Through ${Q_3}$ through \[{Q_3}{P_1}||{Q_5}P\] intersecting QP at ${P_1}$.
Now through PQ, draw ${P_1}{R_1}||PR$intersecting QR at ${R_1}$

On following the above steps of construction, we get the diagram which is required.

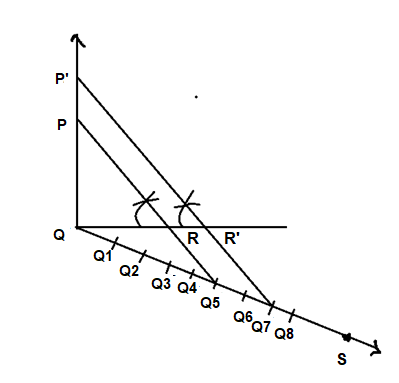
Therefore, the $\vartriangle {P_1}Q{R_1}$ is the required triangle whose sides is $\dfrac{7}{5}$ times the corresponding sides of $\vartriangle PQR$

Note: When we draw the extended ray, we have to make sure the ray is marked according to the highest of the difference factor and the divisions are in equal measurements to each other and the lower value of the difference factor should join the base side of the triangle given in the question.