Question

Draw a ray diagram to show the image formation by a combination of two thin convex lenses to contact. Obtain the expression for the power of this combination in terms of the focal lengths of the lenses.

Answer 1

Hint: Lens are the things which will allow the light to pass through them with convergence or divergence. Depending on whether the lens will converge or diverge the rays they are divided into convex and concave lenses. Their capacity of convergence or divergence is given by power of the lens.

Formula used:
$\eqalign{
  & P = {P_1} + {P_2} \cr
  & P = \dfrac{1}{f} \cr
  & \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f} \cr} $

Complete step by step solution:
When an object is placed in front of the lens the rays from the object passes through the lens and suffers refraction and image is formed. The position where image forms and the nature of the image formed depends upon the type of lens we use.
Here we are using two lenses. Rays passing from the object will go through the convex lens first and suffer refraction. After that a refraction image will be formed which will be at distance ${v_1}$.
Now this image will act as an object for the second lens and image will be formed due to the second lens. That image will be at distance ‘v’ from the lens. The distance of the object from the lens is ‘u’.
Everything is clearly shown in the below diagram.

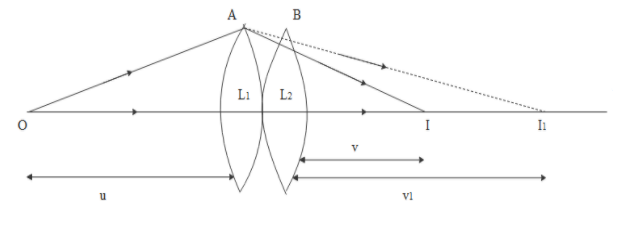
The lenses shown here are very thin and are close to each other. The focal length of the first lens is ${f_1}$ and the focal length of the second lens is ${f_2}$.
We will apply the lens equation for the first lens first.
$\dfrac{1}{{{v_1}}} - \dfrac{1}{u} = \dfrac{1}{{{f_1}}}$
For the second lens we have the equation
$\dfrac{1}{v} - \dfrac{1}{{{v_1}}} = \dfrac{1}{{{f_2}}}$
By adding the above two equations we will get
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
Power of one lens can be given as $P = \dfrac{1}{f}$
So the power of two lens combined will be
$\eqalign{
  & \Rightarrow P = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} \cr
  & \therefore P = {P_1} + {P_2} \cr} $

Note:
The lens refractive index can be varied in such a way that a convex lens can behave as the concave lens without any change in shape. This is when we place the lens in the medium of refractive index greater than the lens refractive index, then the convex lens would change into concave while the concave lens would change into convex. Then focal length will change and power also will change.