Question

Draw a pair of tangents to a circle of radius \[5{\text{ cm}}\] which are inclined to each other at an angle of \[{60^ \circ }\] . Give the justification of construction.

Answer 1

Hint:We use some concepts based on circles and their tangents to solve this problem. A tangent is a line which passes through a circle just touching it at only one point. We get a line by joining this point and centre of the circle, which is perpendicular to the tangent. And from a point outside the circle, only two tangents can be drawn.

Complete step by step solution:
A rough diagram of the structure that we need to construct is like this.

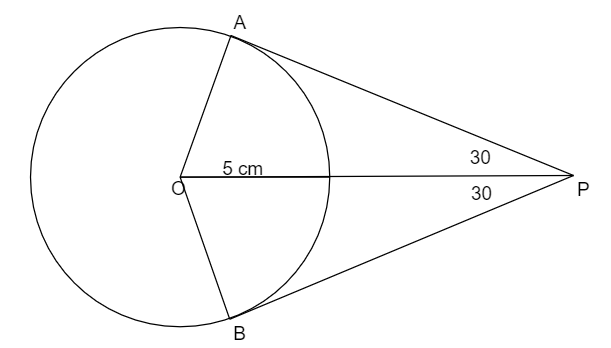
To construct this, we need to follow these steps:
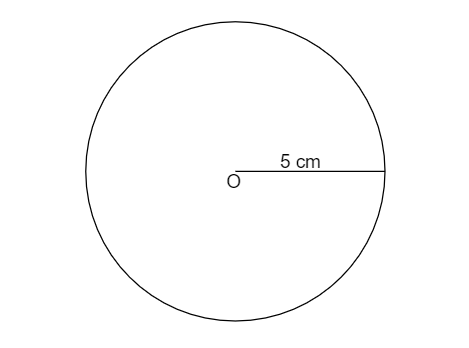
(1) Construct a circle of radius \[5{\text{ cm}}\] with centre as \['{\text{O}}'\]

(2) If you look at the triangle \[\vartriangle APO\] , it is a right-angled triangle with \[\angle APO = {30^ \circ }\] and \[\angle OAP = {90^ \circ }\] .
So, from the trigonometric ratios, \[\sin {30^ \circ } = \dfrac{{AO}}{{OP}}\] \[\left( {\because \sin P = \dfrac{{{\text{length of side opposite to P }}}}{{{\text{hypotenuse}}}}} \right)\]
\[ \Rightarrow \dfrac{{AO}}{{OP}} = \dfrac{1}{2}\] \[\left( {{\text{as sin3}}{0^ \circ } = \dfrac{1}{2}} \right)\]
\[ \Rightarrow \dfrac{5}{{OP}} = \dfrac{1}{2}\]
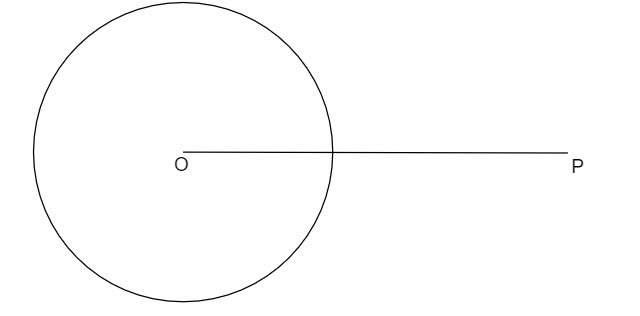
So, \[OP = 10{\text{ cm}}\]
So, mark a point 10 cm away from the centre and mark it as “P”. So, OP = 10

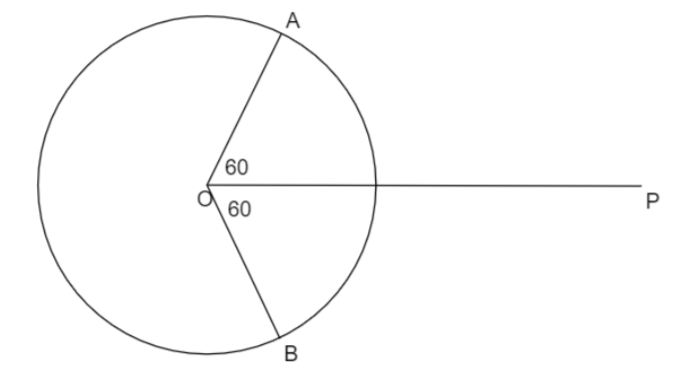
(3) Now, draw two lines from centre to circle such that those two lines are inclined at \[{\text{6}}{0^ \circ }\] to line \[OP\] and mark them as \[A\] and \[B\] .

(4) Join the points AP and BP, and these are the required tangents, which are perpendicular to AO and BO respectively.

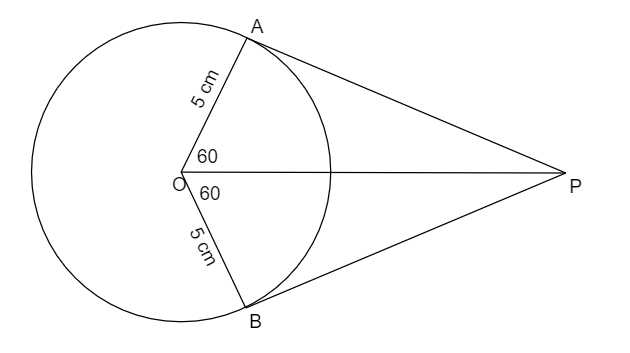
This is the required construction.

Note:
The tangent at a point on a circle, is always perpendicular to line joining that point and centre of the circle. We can also construct using another method. Here, we need to calculate the length of AP using \[\tan {30^ \circ } = \dfrac{{OA}}{{AP}}\] . After getting AP value, with P as centre, and AP as length, cut an arc on a circle, and you will get point A on the circle. Similarly, find point B. join the points and get the lines AP and BP. These are the required tangents to the circle.