Question

Draw a pair of radii $ OA $ and $ OB $ in a circle such that $ \angle BOA = 120^\circ $ . Draw the bisector of $ \angle BOA $ and draw lines perpendicular to $ OA $ and $ OB $ at $ A $ and $ B $ . These lines meet on the bisector of $ \angle BOA $ at a point which is the external point and the perpendicular lines.

Answer 1

Hint: For this construction we first draw a line of given measurement and naming it, draw a fair of radii $ OA $ and $ OB $ in circle, hence we get the required construction asked in the given problem.

Complete step-by-step answer:
The bisector of an angle also called the internal angle bisector, it is a line segment that divides the angle into two equal parts the angle bisectors meet at the centre.
Now step by step construction: -
To draw a pair of radii $ OA $ and $ OB $ in a circle. $ \angle BOA = 120^\circ $ all steps of construction with proper explanation are as follows:
Step 1: Draw a circle with center $ O $ using compass and name its one vertex by $ O $ .

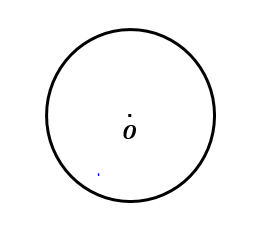
Step 2: In the second step we take a point $ A $ on circle.

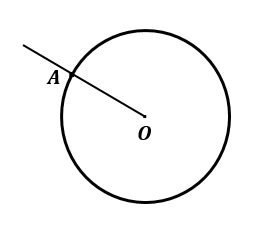
Step 3: Draw an angle of $ 120 $ degree at $ O $ on $ AO $ intersecting circle at $ B $ .

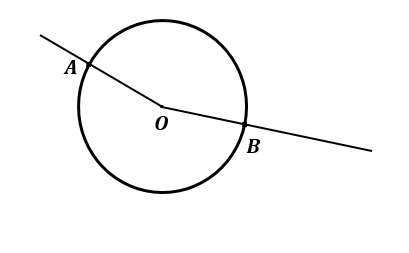
Step 4: draw a $ 90 $ degree angle at $ A $ on $ OA $ and $ B $ at $ OB $ , and intersect each other at $ P $ .
 $ PA $ and $ PB $ are tangents.

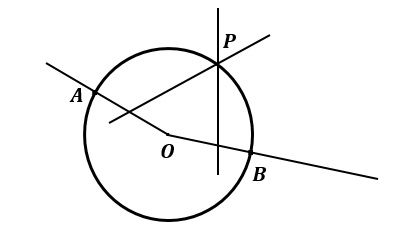
Step 5: Join $ OP $

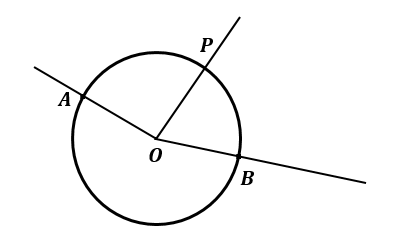
In angle $ AOP $ and angle $ OBP $
Where,
 $ OA $ is equal to $ OB $ and they are the radius of the circle.
In circle $ OP $ is common for both the angle
So,
 $ OP = OP $ (common)
Also,
Angle $ A $ is equal to angle $ B $ and they both are right angle triangle.
So,
 $ \angle A = \angle B = 90^\circ $
 $ \Rightarrow $ by all the condition, we get
 $ \Delta OAP \cong \Delta OBP $
Similarly,
 $ PA = PB $ (They are equal tangents of the circle)
And $ \angle AOP = \angle BOP=60^\circ $
Hence $ OP $ is a bisector of $ \angle BOA $ .

Note: While drawing or doing construction work one must draw a rough figure on the side of the page to understand the steps that are required to construct a required figure. Also one should take measurement regarding construction very carefully to avoid any mistakes. And each step also writes a step of construction explaining how one is proceeding to get final construction.