Question

Draw a line segment ST, measuring 9.5 cm. and construct its perpendicular bisector.

Answer 1

Hint: A line segment is a part of a line that connects two pints. It has a length. We also know that a perpendicular bisector is a line segment which intersects another line perpendicularly and divides it into two equal parts. Using these definitions we can solve this problem. To get a perpendicular bisector we need a line segment.

Complete step-by-step answer:
Let’s first draw a line segment of length 9.5 cm.
We follow these steps.
\[ \bullet \]Draw a line ‘L’
Mark points ‘S’ on it.

\[ \bullet \]Since length is 9.5cm, we measure 9.5 cm using ruler and we mark ‘T’ at exactly 9.5cm from point ‘S’.

Thus we have a line segment ‘ST’ of length 9.5cm.
Now to construct the perpendicular bisector, we follow these steps.
\[ \bullet \] Since we have a line segment ‘ST’. Take ‘A’ as a centre and radius more than half of the length of AB, draw two arcs, one on either side of ‘ST’.

\[ \bullet \] Similarly take ‘T’ as centre and the same length taken in the previous step, draw two arcs, cutting the previously drawn arcs. We get points ‘A’ and ‘C’.
 

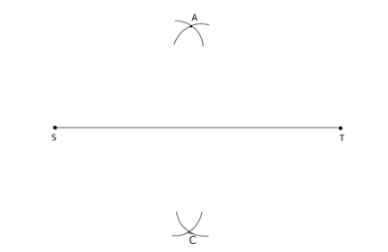
\[ \bullet \] In the final steps we join the points ‘A’ and ‘C’ by a straight line. This straight line intersects the line ‘ST’ at ‘P’.

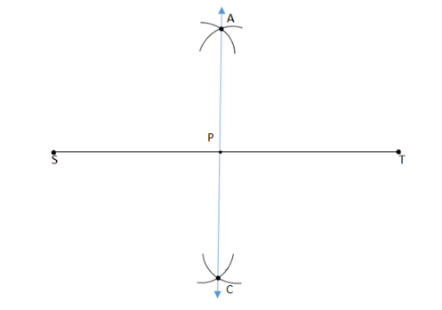
Note: In drawing the bisector line, we need to construct arcs and we need to take more than half of the length of line ‘ST’ while drawing an arc. In this problem we have a length of ‘ST’ is 9.5 cm and half of it is 4.75 cm. In both cases while taking ‘S’ and ‘T’ as a centre for drawing an arc we take the radius length more than 4.75 cm.