Question

Draw a line segment PQ = 4cm. Draw a perpendicular bisector to PQ.

Answer 1

Hint: In this question, we need to construct a perpendicular bisector of the line PQ. For this, we will need a compass and ruler. First we will draw a line segment PQ = 4cm and then use the compass to draw arcs from both ends to both sides of the line. Then we will join points formed to get the perpendicular bisector. We will draw a perpendicular bisector step by step with written steps of construction.

Complete step-by-step answer:
Here, we need to draw a perpendicular bisector of the line PQ. Since PQ is given as 4cm. So following are the steps of construction involved in making a perpendicular bisector.
(i) Draw a line segment PQ = 4cm.

(ii) Now, open the compass more than half the length of the side PQ. With P as center and radius equal than half of PQ, draw an arc on both sides of PQ.

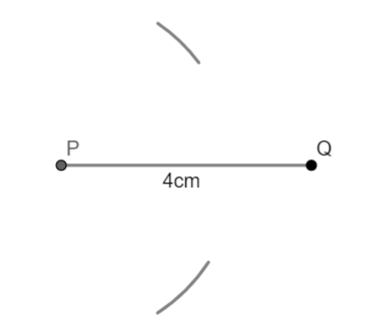
(iii) Now with Q as center and same radius as taken in 2, draw arcs on both sides of PQ. Let these arcs intersect each other at point A and B.

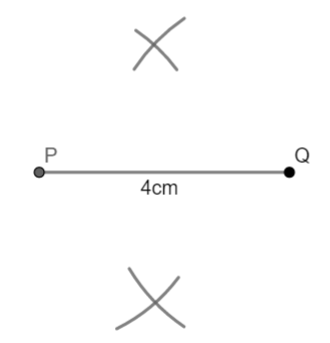
(iv) Join A and B. The line AB cuts the line segment PQ at the point O.

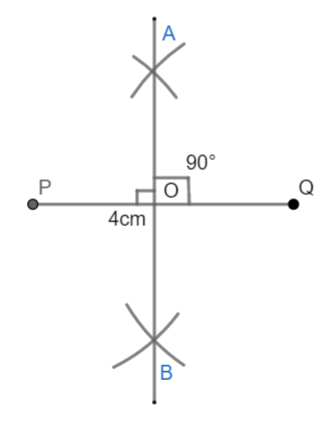
Here, OP = OQ and $\angle AOQ={{90}^{\circ }}$. Thus the line AB is a perpendicular bisector of AB.

Note: Students should note that the perpendicular bisector of any line is a line which cuts the line segments into two equal parts and is perpendicular to the line segment. While drawing arcs, make sure that the compass is opened more than half of PQ otherwise arcs will not cut. Students should check the final diagram seeing if OP = OQ and $\angle AOQ={{90}^{\circ }}$.