Question

Draw a line segment $ \overline {AB} $ and then draw a perpendicular bisector to it.

Answer 1

Hint: We have to geometrically construct a line segment and a perpendicular bisector to it. Bisecting a line segment means dividing it into two equal parts. Since we have to draw a perpendicular bisector of the line segment $ \overline {AB} $ , the perpendicular bisector will pass through the midpoint of $ \overline {AB} $ . We have to draw a line at $ {90^o} $ at this midpoint which will be the perpendicular bisector.

Complete step by step solution:
We will carry out this geometric construction using ruler, pencil and compasses.
We are showing the construction first which is followed by the steps which are to be followed to construct this.

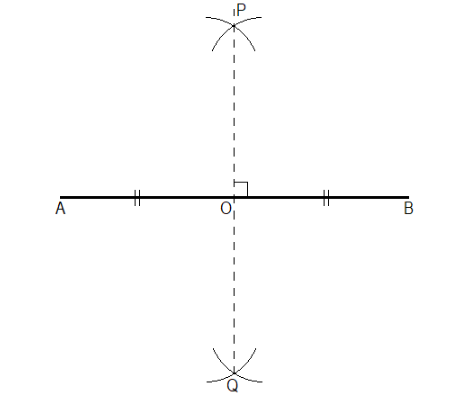
We have $ \overline {PQ} \bot \overline {AB} $ and $ \overline {AO} = \overline {BO} $ .
The steps for the construction are as follows-
First we draw a line segment $ \overline {AB} $ using a ruler. Since no length is given we can draw a line segment of any length as suitable.
Now we have to find the midpoint of $ \overline {AB} $ . For this we use the compasses. Keeping the point of the compasses at point $ A $ and length of the compasses more than half of the length of $ \overline {AB} $ , we draw an arc above the line segment $ \overline {AB} $ and one arc below the line segment $ \overline {AB} $ .
Similarly, keeping the length of the compasses the same, we draw arcs above and below the line segment from point $ B $ such that these arcs cut the arcs drawn from point $ A $ .
Now we get two points, let us say point $ P $ and $ Q $ , which are the meeting points of the arcs above and below the line segment. We join these two points. The line $ \overline {PQ} $ cuts the line $ \overline {AB} $ at point $ O $ .
The resulting line $ \overline {PQ} $ is the required perpendicular bisector of the line $ \overline {AB} $ .

Note: Since the length of the line segment $ \overline {AB} $ is not given we can assume it to be of any length. Drawing a perpendicular is the same as drawing an angle of $ {90^o} $ at a point on the line. The length of the compasses should be kept the same for whole construction for accurate results. At the end of the construction we can use a ruler and a protractor to check the measurements.