Question

Draw a graph of the linear equation \[y = - 2x - 7\].

Answer 1

Hint: Straight lines graphs are formed by the linear equation. Linear equation is an equation where two expressions are set equal to each other, when we find the values of the pairs and plot it on a graph paper, it forms a straight line and all the pairs lie on this straight line.

Complete step by step solution:
In this problem, we have to draw a graph of linear equations. To find it, firstly, we need to find the values of x and y. We can assume the values of x and then, we will find the value of y, by this we will get our points to locate in the graph.
Part-1 Let us assume $ x = - 2 $ , now we will substitute the value of x into the given equation\[y = - 2x - 7\],
 $
   \Rightarrow y = - 2( - 2) - 7 \\
   \Rightarrow y = - 2 \times ( - 2) - 7 \\
   \Rightarrow y = 4 - 7 \\
   \Rightarrow y = - 3 \;
  $
Now, the value of y when $ x = - 2 $ is $ - 3 $ .
Part-2 Let us assume $ x = 0 $ , after substituting the value of x in the given equation, we get,
 $
   \Rightarrow y = - 2(0) - 7 \\
   \Rightarrow y = - 2 \times 0 - 7 \\
   \Rightarrow y = - 7 \;
  $
Now, the value of y when $ x = 0 $ is $ - 7 $ .
Part-3 Let us assume $ x = 2 $ and after substituting the value of x in the given equation, we get,
 $
   \Rightarrow y = - 2(2) - 7 \\
   \Rightarrow y = - 2 \times 2 - 7 \\
   \Rightarrow y = - 4 - 7 \\
   \Rightarrow y = - 11 \;
  $
Now, the value of y when $ x = 2 $ is $ - 11 $ .
Part-4 Let us assume $ x = 4 $ and after substituting the value of x in the given equation, we get,
 $
   \Rightarrow y = - 2\left( 4 \right) - 7 \\
   \Rightarrow y = - 2 \times 4 - 7 \\
   \Rightarrow y = - 8 - 7 \\
   \Rightarrow y = - 15 \;
  $
Now, the value of y when $ x = 4 $ is $ - 15 $ .
Now, the points of the coordinates are $ \left( { - 2, - 3} \right),\left( {0, - 7} \right),\left( {2, - 11} \right),\left( {4, - 15} \right) $ . Hence, the graph of the linear equation $ y = - 2x - 7 $ is,

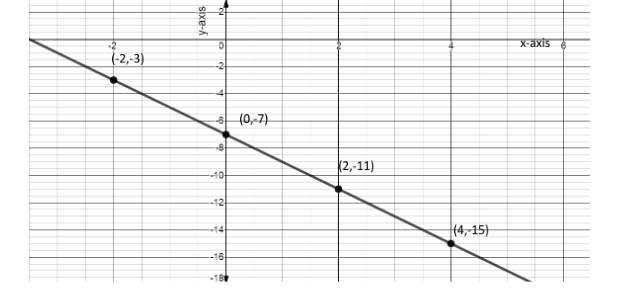
Note: Image result for graph of two variables
For an equation with two variables, x and y , we need a graph with two axes: an x -axis and a y -axis. We will use the Cartesian plane, in which the x -axis is a horizontal line and the y -axis is a vertical line. Where the two axes cross is called the origin.