Question

Draw a diagram showing all components of forces acting on a vehicle moving on a curved banked road. Write the necessary equation for maximum safety speed and state the significance of each term involved in it.

Answer 1

Hint:Banking of roads: When a vehicle goes around the curved track at a reasonable speed without skidding, it is managed with it by raising the outer edge of the track a little above the inner edge, this is done to reduce the wear and tear of the car tyres and also the risk of skidding.

Complete step by step answer:
We have been asked to draw a diagram showing all components of forces acting on a vehicle moving on a curved banked road and also to write the necessary equation for maximum safety speed and the significance of each term involved in it. Now, let us consider a car having weight Mg moving round a curved path of radius r with a speed v on a curved banked road through angle $\theta $.

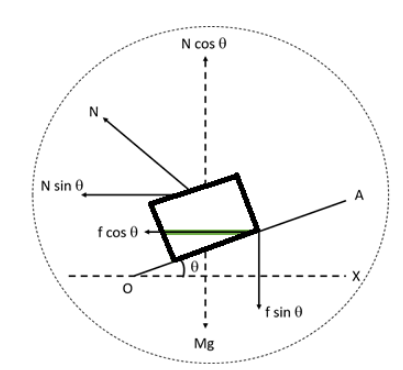
The forces which will act on the vehicle are:
1. The weight Mg which is acting vertically downwards.
2. The normal reaction of the road N, which is perpendicular to the road surface.
3. The frictional force f, which is along the inclined surface of the road.

Necessary equation for maximum safety speed:
Normal N and friction f have perpendicular components \[Ncos\theta \] which is vertically up and \[fsin\theta \] which is vertically down. And the horizontal components \[Nsin\theta \] and \[fcos\theta .\] Now, if is the maximum safe speed is without skidding, then,
$\dfrac{{m{V^2}_{\max }}}{r} = N\sin \theta + {f_s}\cos \theta $
$
\Rightarrow \dfrac{{m{V^2}_{\max }}}{r} = N\sin \theta + {\mu _s}N\cos \theta \\
\Rightarrow\dfrac{{m{V^2}_{\max }}}{r} = N(\sin \theta + {\mu _s}\cos \theta )......eq.(1) \\ $
Also, the $N\cos \theta = mg + {f_s}\sin \theta $
$mg = N(\cos \theta - {\mu _s}\sin \theta ).......eq.(2)$
On dividing equation (1) by (2), we get
$
\dfrac{{m{V^2}_{\max }}}{{r(mg)}} = \dfrac{{N(\sin \theta + {\mu _s}\cos \theta )}}{{N(\
\theta - {\mu _s}\sin \theta )}} \\
\Rightarrow\dfrac{{{V^2}_{\max }}}{{rg}} = \dfrac{{\sin \theta + {\mu _s}\cos \theta }}{{\cos \theta - {\mu _s}\sin \theta }} \\
\Rightarrow\dfrac{{{V^2}_{\max }}}{{rg}} = \dfrac{{\tan \theta + {\mu _s}}}{{1 - {\mu _s}\tan \theta }} \\
 $
\[\therefore{V_{\max }} = \sqrt {rg[\dfrac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}]} \]

Thus, the equation for maximum safety speed for the vehicle moving on the curved banked road is, \[{V_{\max }} = \sqrt {rg[\dfrac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}]} \]
where, \[r{\text{ }} = \] radius of curved road
$\theta = $angle of banking
${\mu _s} = $ coefficient of friction between road and tyres

Note: Students should carefully draw the diagram. And don’t forget about the frictional force, as most of the time we neglect the frictional force, but here as we are asked about all the forces we are supposed to consider that also. The maximum safety speed of a vehicle on a curve depends upon friction between tyres and roads. It depends on the angle through which the road is banked. It is independent of the mass of the vehicle.