Question

Draw a diagram for the following statement and prove the result:
In an isosceles triangle, the median joining the vertex (formed by intersection of equal sides) to the midpoint of the opposite side is an altitude.

Answer 1

Hint: To solve these questions, congruence of triangles can be used along with the properties of the triangle that is mentioned in the question. The question will be easily solved after drawing the diagram and including all the information in it given in the question.

Complete step-by-step solution:
First draw the figure with all the information provided in the question, in this case, the figure will be as given below:

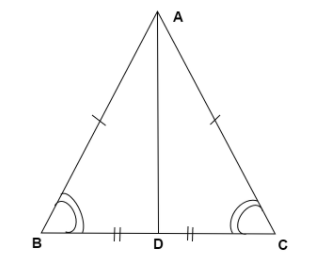
Given, in the triangle $\Delta ABC$ :
 $AB = AC$ , since it is given according to the question that $\Delta ABC$ is isosceles.
 $BD = CD$ , since $\;AD$ is the median and a median divides the side it is projected on in two equal parts.
$\angle B = \angle C$ , since the angles opposite to the equal sides are equal in an isosceles triangle.
Now taking $\Delta ABD$and $\Delta ADC$ separately,
$AB = AC$ , since these are the two equal sides of the isosceles $\Delta ABC$
 $BD = CD$ , as the median divides the line $\;BC$ into two equal parts
$\angle B = \angle C$ , angles opposite to the equal sides of $\Delta ABC$
From the above three conclusions, we can conclude that $\Delta ABD$ and $\Delta ADC$ are congruent triangles, therefore:
$\Rightarrow \Delta ABD \cong \Delta ADC$ (By Side Angle Side Theorem$\left( {SAS} \right)$)
Further, from the above result, we can conclude that,
$\Rightarrow \angle ADB = \angle ADC$ (Common parts of Congruent Triangles$(CPCT)$) $.....(i)$
Since, $\;BDC$ is a straight line therefore
$\angle BDC = {180^\circ }$
Now, $\angle BDC$ consists of two angles, $\angle ADB$ and $\angle ADC$ , so we get
$\Rightarrow \angle ADB + \angle ADC = {180^\circ }$
Substituting equation $(i)$ in the above equation, we get
$\Rightarrow 2\angle ADB = {180^\circ }$
Dividing both the sides by $2$ , we get
$\Rightarrow \angle ADB = {90^\circ }$
Again $\angle ADB$ and $\angle ADC$ are equal from equation $(i)$ , therefore
$\Rightarrow \angle ADB = \angle ADC = {90^\circ }$
An altitude is a line that makes an angle of $\angle {90^\circ }$ with the line it is projected on, therefore it is proved that $\;AD$ is the altitude of the isosceles triangle $\Delta ABC$ .

Note: While applying the Side Angle Side congruence theorem $\left( {SAS} \right)$ , make sure that the angle considered for the congruence is the angle formed by the intersection of the two sides which are considered for the congruency. It becomes very easy to solve these questions if the diagram is drawn first, according to the question.