Question

Draw a circle with centre O and radius \[2.5{\text{ }}cm.\] Draw a chord AB passing through its centre. Then \[\angle \]AOB is.

Answer 1

Hint: To solve this question, we will start with constructing the diagram of circle of radius \[2.5{\text{ }}cm.\]Now to find the \[\angle \]AOB, we will construct a chord AB in the circle, which is a diameter as diameter passes through the centre and it makes \[180^\circ \] at the centre of the circle. Hence, we will get our required answer.

Complete step-by-step answer:
We have been asked to draw a circle with centre O and radius \[2.5{\text{ }}cm.\] And we need to draw a chord AB passing through its centre. Then we also need to find the \[\angle \]AOB.
So, to draw the circle, first we will take \[2.5{\text{ }}cm\] in a compass from the ruler as radius and then with the help of the compass we will draw a circle with centre O and radius \[2.5{\text{ }}cm.\]

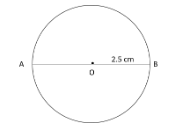
Here, in the diagram we can see that chord AB is passing through the centre O.
We know that a line passing through the centre is called diameter. So, AB is the diameter of the circle with centre O. And we know that diameter makes \[180^\circ \] at the centre of the circle.
Thus, \[\angle \]AOB \[ = {\text{ }}180^\circ \]

Note: In the question, the chord word is mentioned. Chord is the straight-line segment that passes through two points, whose endpoints lie on the circle only. So, it can be formed by joining any two points in a circle. And the biggest chord in a circle is a diameter which passes through the centre of the circle.