Question

Draw a circle of radius 6 cm from a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Answer 1

Hint: Try to do the construction step wise by first constructing the circle and then the pair of tangents with respect to the lengths given.

Complete step-by-step answer:

We can perform asked construction as follows:
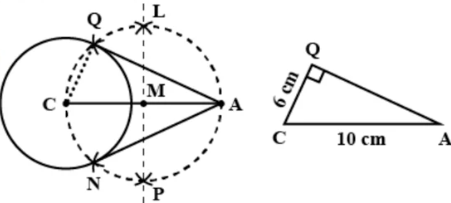
First of all, we’ll construct a circle of 6 cm radius with the help of a compass.
Name the centre as C.
Locate a point A which should be 10 cm away from the centre C.
Draw a perpendicular line bisecting the line, joining points C and A. Let’s name this mid-point as M.
Now, draw another circle with centre at M and radius 5 cm which is nothing but $\dfrac{{AC}}{2}$ .
Let’s say this new circle cuts the previous circle at points N and Q then draw the lines AQ and AN, which are our external tangents.
Since, $\vartriangle CQA$ is right angle triangle at $\angle CQA$ , let’s use the Pythagoras theorem
$
   \Rightarrow {(CQ)^2} + {(QA)^2} = {(CA)^2} \\
   \Rightarrow {(QA)^2} = {(CA)^2} - {(CQ)^2} \\
   \Rightarrow {(QA)^2} = {(10)^2} - {(6)^2} \\
   \Rightarrow {(QA)^2} = 100 - 36 \\
   \Rightarrow {(QA)^2} = 64 \\
   \Rightarrow QA = 8 \\
$
Hence, the length of the tangent is 8 cm.

Note: Here, while taking the square root of QA we have considered only positive signs. One can think why is it so? Why only positive signs? It’s because the reason that QA is a line segment which has its own length and length can’t be negative.